Cho 2 phương trình \(x^3+2x^2+3x+4=0\) và \(x^3-8x^2+23x-26=0\).CMR mỗi phương trình trên có đúng 1 nghiệm,tính tổng 2 nghiệm đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2021
1.
Đặt \(f\left(x\right)=\left(m^2+1\right)x^3-2m^2x^2-4x+m^2+1\)
\(f\left(x\right)\) xác định và liên tục trên R
\(f\left(x\right)\) có bậc 3 nên có tối đa 3 nghiệm (1)
\(f\left(0\right)=m^2+1>0\) ; \(\forall m\)
\(f\left(1\right)=\left(m^2+1\right)-2m^2-4+m^2+1=-2< 0\) ;\(\forall m\)
\(\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) (2)
\(f\left(2\right)=8\left(m^2+1\right)-8m^2-8+m^2+1=m^2+1>0\)
\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\) (3)
\(f\left(-3\right)==-27\left(m^2+1\right)-18m^2+12+m^2+1=-44m^2-14< 0\)
\(\Rightarrow f\left(-3\right).f\left(0\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-3;0\right)\) (4)
Từ (1); (2); (3); (4) \(\Rightarrow f\left(x\right)=0\) có đúng 3 nghiệm phân biệt
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2021
2.
Đặt \(t=g\left(x\right)=x.cosx\)
\(g\left(x\right)\) liên tục trên R và có miền giá trị bằng R \(\Rightarrow t\in\left(-\infty;+\infty\right)\)
\(f\left(t\right)=t^3+m\left(t-1\right)\left(t+2\right)\)
Hàm \(f\left(t\right)\) xác định và liên tục trên R
\(f\left(1\right)=1>0\)
\(f\left(-2\right)=-8< 0\)
\(\Rightarrow f\left(1\right).f\left(-2\right)< 0\Rightarrow f\left(t\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)
\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm với mọi m
CM
11 tháng 4 2017
a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình 
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 
AH
Akai Haruma
Giáo viên
25 tháng 7 2021
Câu 3:
$\Delta=2015^2-4.2013.2=2011^2$
Do đó pt có 2 nghiệm:
$x_1=\frac{2015+2011}{2.2013}=1$
$x_2=\frac{2015-2011}{2.2013}=\frac{2}{2013}$
Đáp án B.
AH
Akai Haruma
Giáo viên
25 tháng 7 2021
Câu 4:
Theo định lý Viet, tổng các nghiệm của pt là:
$S=\frac{-b}{a}=\frac{-3}{1}=-3$
Đáp án B.
CM
9 tháng 11 2017
a) Thay x = 3 2 vào (1) và (2) thấy thỏa mãn nên x = 3 2 là nghiệm chung của cả hai PT đã cho.
b) Thay x = -5 vào (2) thấy thỏa mãn nên x = -5 là nghiệm của (2). Thay x = -5 vào (1) thấy không thỏa mãn nên x = -5 không là nghiệm của (1).
c) Cách 1. Tìm được tập nghiệm của (1) và (2) lần lượt là S 1 = { 1 ; 3 2 } và S 2 = { - 5 ; 3 2 }
Vì S 1 ≠ S 2 Þ Hai phương trình không tương đương nhau.
Cách 2. Theo ý b, x = -5 là nghiệm của (2) nhưng không là nghiệm của (1) nên hai PT không có cùng tập nghiệm.
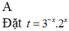
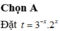
Lời giải:
Định lý: điều kiện đủ để phương trình \(f(x)=0\) có ít nhất một nghiệm trên khoảng \((a;b)\) là \(f(x)\) liên tục trên \([a,b]\) và \(f(a)f(b)<0\).
Bây giờ xét \(\left\{\begin{matrix} f(x)=x^3+2x^2+3x+4\\ g(x)=x^3-8x^2+23x-26\end{matrix}\right.\)
Ta thấy hai hàm trên liên tục trên \(R\). Hơn nữa:\(\left\{\begin{matrix} f(-2)f(0)<0\\ g(3)g(4)<0\end{matrix}\right.\)
Do đó \(f(x) =0\) có ít nhất một nghiệm \(x_1\in (-2,0)\) và \(g(x)=0\) có ít nhất một nghiệm \(x_2\in (3,4)\)
Lại có \(f'(x)=3x^2+4x+3>0\forall x\in\mathbb{R}\) và \(g'(x)=3x^2-16x+23>0\forall x\in\mathbb{R}\) nên hai hàm luôn đồng biến .
Do đó, cả hai PT đều có duy nhất một nghiệm.
Vì nó chỉ có duy nhất một nghiệm nên có thể tính trực tiếp (hoặc sử dụng phương pháp Cardano ta suy ra tổng hai nghiệm của chúng là \(x_1+x_2=2\)
lớp mấy vậy bạn