Giải phương trình:
2x3+9x2+7x-6=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 11 2018
Đặt y = 2 x 3 - 9 x 2 + 12 x - 4
Ta có f x = f x , x ≥ 0 f - x , x < 0 .
Do f x là hàm số chẵn nên đồ thị đối xứng qua trục tung. Như vậy đồ thị của nó gồm hai
Phần bên phải trục tung của đồ thị hàm số y = f(x)
Đối xứng phần đồ thị trên qua trục tung
Ta có: 2 x 3 - 9 x 2 + 12 x = m
⇔ 2 x 3 - 9 x 2 + 12 x - 4 = m - 4
Phương trình đã cho có 6 nghiệm phân biệt.
Đường thẳng y = m - 4 cắt đồ thị f x hàm số tại 6 điểm phân biệt
0 < m - 4 < 1 nên 4 < m < 5
Đáp án B
CM
24 tháng 12 2019
+Trước tiên từ đồ thị hàm số y= 2x3- 9x2+12x , ta suy ra đồ thị hàm số y= 2 x 3 - 9 x 2 + 12 x như hình dưới đây:
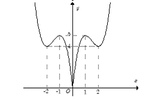
+ Phương trình 2 x 3 - 9 x 2 + 12 x + m = 0 và đường thẳng y= -m
+ Dựa vào đồ thị hàm số y = 2 x 3 - 9 x 2 + 12 x , yêu cầu bài toán trở thành:
4< -m< 5 hay -5<m< -4.
Chọn B.
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 5 2021
Đặt \(f\left(x\right)=2x^3-9x^2+12x-2-m\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(\forall m\in\left(2;3\right)\) ta có:
\(f\left(0\right)=-2-m< 0\)
\(f\left(1\right)=3-m>0\)
\(\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) (1)
\(f\left(2\right)=2-m< 0\)
\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\) (2)
\(f\left(3\right)=7-m>0\)
\(\Rightarrow f\left(2\right).f\left(3\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(2;3\right)\) (3)
Từ (1); (2); (3) \(\Rightarrow f\left(x\right)\) luôn có 3 nghiệm dương pb
PT
1
CM
9 tháng 1 2019
9x2 + 4x – 3 – (3x + 2)2 > 0
⇔9x2 + 4x – 3 – (9x2 + 12x + 4) > 0
⇔ 9x2 + 4x – 3 – 9x2 – 12x – 4 > 0
⇔ – 8x > 7 ⇔ x < 7/-8 ⇔ x < -7/8
Tập nghiệm: S = {x|x < -7/8}
PT
1
YY
2
10 tháng 2 2022
a, \(x^4-x^2-2=0\Leftrightarrow x^4-2x^2+x^2-2=0\)
\(\Leftrightarrow x^2\left(x^2-2\right)+\left(x^2-2\right)=0\Leftrightarrow\left(x^2+1>0\right)\left(x^2-2\right)=0\Leftrightarrow x=\pm\sqrt{2}\)
b, \(\Leftrightarrow x^2\left(x^2+2x+1\right)=0\Leftrightarrow x^2\left(x+1\right)^2=0\Leftrightarrow x=0;x=-1\)
c, \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1>0\right)=0\Leftrightarrow x=1\)
d, \(\Leftrightarrow6x^2-3x-4x+2=0\Leftrightarrow\left(3x-2\right)\left(2x-1\right)=0\Leftrightarrow x=\dfrac{2}{3};x=\dfrac{1}{2}\)
R
10 tháng 2 2022
a)
/ \(x^4+x^2-2=0\)
\(\Leftrightarrow\left(x^2\right)^2-x^2+2x^2-2=0\\ \Leftrightarrow x^2\left(x^2-1\right)+2\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x-1\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+2=0\\x+1=0\\x-1-0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
20 tháng 1 2017
a, 3x2 - 8x2 - 2x+3=0
2x(3-8) - 2x+3=0
2x5 - 2x+3=0
2x5 - 2x=0-3=
2x5 - 2x=-3
2x(5-x)=-3
5-x=-3/2
5-x=1,5
x=5-1,5
x=3,5
Nhân 4 lên rồi đặt 2x=y
\(8x^3+9.4x^2+7.4x-24=0\)
\(\Leftrightarrow y^3+9y^2+14y-24=0\) cho gọn hệ số dẽ ghép
\(y^2\left(y-1\right)+10y\left(y-1\right)+24y-24=\left(y-1\right)\left(y^2+10y+24\right)\)
\(\Leftrightarrow\left[\begin{matrix}y-1=0\Rightarrow y=1\Rightarrow x=\frac{1}{2}\\y^2+10y+24=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow y^2+2.5y+25=\left(y+5\right)^2=1\Rightarrow\left[\begin{matrix}y=-6\\y=-4\end{matrix}\right.\Rightarrow\left[\begin{matrix}x=-3\\x=-2\end{matrix}\right.\)
Kết luận: \(\left[\begin{matrix}x=\frac{1}{2}\\x=-2\\x=-3\end{matrix}\right.\)