Cho tứ giác ABCD ngoại tiếp đường tròn tâm O; gọi M,N,P,Q lần lượt là tiếp điểm của đường tròn (O) với AB, BC, CD, DA. AN cắt (O) tại E, AP cắt (O) tại F. CMR: ME, AC, QF đồng quy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 5 2017
Đáp án A
Vì tứ giác ABCD là hình bình hành và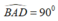 
nên ABCD là hình chữ nhật.
Gọi O là giao điểm hai đường chéo.
Theo tính chất hình chữ nhật ta có:
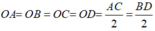
Do đó, O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD.
9 tháng 5 2023
a: góc IED+góc ICD=180 độ
=>IEDC nội tiếp
b: góc ECI=góc BDA=1/2*sđ cung BA
=>góc ECI=góc BCI
=>CI là phân giác của góc BCE
17 tháng 2 2022
a: Xét tứ giác MBHC có
\(\widehat{MBH}+\widehat{MCH}=180^0\)
Do đó: MBHC là tứ giác nội tiếp
b: Sửa đề: \(MC\cdot MP=MB\cdot MN\)
Xét ΔMCP vuông tại C và ΔMBN vuông tại B có
\(\widehat{BMN}\) chung
Do đó: ΔMCP\(\sim\)ΔMBN
Suy ra: MC/MB=MP/MN
hay \(MC\cdot MN=MB\cdot MP\)
20 tháng 3 2023
Sửa đề: Hai đường cao BN,CK
a: góc AKH+góc ANH=180 độ
=>AKHN nội tiếp
Tâm là trung điểm của AH
b: Xet ΔANB vuông tại N và ΔAKC vuông tại K có
góc A chung
=>ΔANB đồng dạng với ΔAKC
=>NB/KC=AN/AK
=>NB*AK=AN*KC
c: góc BKC=góc BNC=90 độ
=>BKNC nội tiếp
d: Xét ΔACB co
BN,CK là đường cao
BN cắt CK tại H
=>H là trực tâm
=>AH vuông góc CB
31 tháng 5 2021
Ta có \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BCEF nội tiếp đường tròn đường kính BC. Tâm I của đường tròn này là trung điểm của BC