Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đặt các chữ cái vào các ô trống:
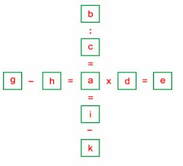
Theo đầu bài ta có các chữ cái khác nhau biểu thị các số khác nhau. Do đó: a ≠ 1; c ≠ 1; d ≠ 1; b > 1; e > 1. Vì 9 = 1 x 9 = 3 x 3 nên b ≠ 9 và e ≠ 9; và 7 = 1 x 7 nên b ≠ 7 và e ≠ 7.
Do đó: b = 6 và e = 8 hoặc b = 8 và e = 6.
Vì 6 = 2 x 3 và 8 = 2 x 4 nên a = b : c = e : d = 2.
Trong các ô trống a, b, c, d, e đã có các số 2, 3, 4, 6, 8; do đó chỉ còn các số 1, 5, 7, 9 điền vào các ô trống g, h, i, k.
* Nếu e = 6 thì g = 7 và h = 1. Do đó a = i - k = 9 - 5 = 42 (loại).
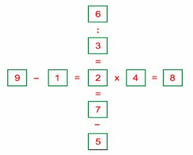
* Nếu e = 8 thì g = 9 và h = 1. Do đó a = i - k = 7 - 5 = 2 (đúng). Khi đó: b = 6 và c = 3. Kết quả:
B = {a \(\in\) Z| (a2 + 3a + 6) ⋮ (a + 3)}
a2 + 3a + 6 ⋮ a + 3
a.(a + 3) + 6 ⋮ a + 3
6 ⋮ a + 3
a + 3 \(\in\) Ư(6) = {-6; -3; -2; -1; 1; 2; 3; 6}
Lập bảng ta có:
| a + 3 | - 6 | - 3 | -2 | -1 | 1 | 2 | 3 | 6 |
| a | - 9 | - 6 | -5 | -4 | -2 | -1 | 0 | 3 |
Theo bảng trên ta có: a \(\in\) {-9; -6; -5; -4; -2; -1; 0; 3}
B = {-9; -6; -5; -4; -2; -1; 0; 3}
Vậy số phần tử tập B là 8 phần tử.
Để có số tận cùng là 1,3,4,5, ko có tích 2 chữ số trong những số đã cho thoả mãn
Để tích có số tận cùng là 2 có 3x4 thoả mãn
Để tích có số tận cùng là 6 có 2x3 thoả mãn
* Xét a3x4=bc2 => a>2, a=5 hoặc 6 thử tính rồi loại
* Xét a4x3=bc2 => a>3 => a=5 hoặc 6, thử rồi chọn đc a=5
* Xét a2x3=bc6 => a>3 => a=4 hoặc 5 hoặc 6 tính rồi loại
* Xét a3x2=bc6 => a>4 => a=5 thử rồi loại
Vậy kết quả 54x3=162 là duy nhất
ĐPCM
Để có số tận cùng là 1,3,4,5, ko có tích 2 chữ số trong những số đã cho thoả mãn Để tích có số tận cùng là 2 có 3x4 thoả mãn Để tích có số tận cùng là 6 có 2x3 thoả mãn * Xét a3x4=bc2 => a>2, a=5 hoặc 6 thử tính rồi loại * Xét a4x3=bc2 => a>3 => a=5 hoặc 6, thử rồi chọn đc a=5 * Xét a2x3=bc6 => a>3 => a=4 hoặc 5 hoặc 6 tính rồi loại * Xét a3x2=bc6 => a>4 => a=5 thử rồi loại Vậy kết quả 54x3=162 là duy nhất ĐPCM
Tất cả các bạn đều nhận ra một phương án điền số: a = 1; b = 9; c = 5; d = 4; e = 6; g = 10; h = 3; i = 1; k = 8; l = 7. Từ đó sẽ có các phương án khác bằng cách:
1) Đổi các ô b và c.
2) Đổi các ô k và l.
3) Đổi các ô d và h.
4) Đổi đồng thời cả 3 ô a, b, c cho 3 ô i, k, l.
Như vậy các bạn sẽ có 16 cách điền số khác nhau.
