Cho tam giác ABC có M,N,P lần lượt là trung điểm của AB, AC, BC.
d1, d2 lần lượt là đường trung trực của AB và AC.
Gọi E là giao điểm của d1 và d2.
Chứng minh EP là đường trung trực của BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ba đường thẳng cùng đi qua một điểm và điểm đó cách đều 3 đỉnh của tam giác (sẽ được chứng minh ở chương sau lớp 7)
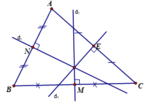

E nằm trên đường trung trực của AB
=>EA=EB
E nằm trên đường trung trực của AC
=>EA=EC
=>EA=EB=EC
=>E là tâm đường tròn ngoại tiếp ΔABC(1)
Ta có: ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC(2)
Từ (1) và (2) suy ra E là trung điểm của BC
chỉ cầm CM: EP vuông góc vs BC là xong rùi đó !
làm thế nào để chứng minh EP vuông góc với BC vậy?