Cho tam giác ABC cân tại A có Â = 20o. Các điểm M, N theo thứ tự thuộc các cạnh bên AB, AC sao cho góc BCM = 50o, góc CBN = 60o.Tính góc MNA.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+) Vẽ góc BCK=600; CK cắt BN tại I. Khi đó tam giác BIC đều => BC = BI = IC
Xét tam giác BIK và BIN có: góc KBI = CIN ( =200 ); BI = IC; góc KIB = NIC ( đối đỉnh ) => tam giác BIK = CIN ( g - c - c)
=> IK = IN mà góc KIN = 600 Nên tam giác KIN đều => NK = IN ( * )
+) Tam giác ABC cân tại A có góc A= 200 => góc ABC = ACB ( 1800- 1200 ): 2=800
+) Xét tam giác BMC có: góc MBC = 800; góc BCM = 500 => góc BMC = 500 => tam giác BMC cân tại B => BC = CM mà BC = BI
nên BI = BM => tam giác BMI cân tại B => góc BIM = ( 1800 - MBI ):2 =800
Ta có góc BIC + BIM + MIK = 1800 => 600 + 800 + MIK = 1800 => góc MIK bằng 400
Mà có góc BKC = 1800 - ( KBC + KCB ) = 400
=> góc MIK = BKC => tam giác MIK cân tại M => MK = MI ( ** )
Từ ( * ); ( ** ) => NM là đường trung thực của KI lại có tam giác NIK đều => góc MNI = KNI :2 = 300
+) góc BNC = 1800 - ( NBC + NCB ) = 400
Ta có góc MNA + MNI + INC = 1800 =>MNA + 300 + 400 = 1800 => goác MNA = 1100

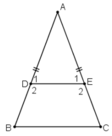
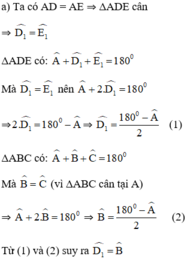
Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
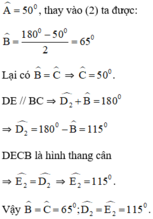


Hình thì chú tự vẽ nhé, anh đây mệt lắm.
Xét góc BMC có:
góc DMB + góc EMC = 180 độ - góc DME (1)
Xét tam giác BDM có:
góc BDM + góc DMB = 180 độ - góc B (2)
Mà góc B = góc DME (3)
Từ (1), (2), (3) => góc EMC = góc BDM
Xét tam giác BDM và tam giác CME có:
góc EMC = góc BDM (cmt)
góc B = góc C (tam giác ABC cân tại A)
=>tam giác BDM~tam giác CME (g - g)
+) Vẽ góc BCK = 60o ; CK cắt BN tại I. Khi đó, tam giác BIC đều => BC = BI = CI
Xét tam giác BIK và CIN có: góc KBI = CIN (=20o) ; BI= CI; góc KIB = NIC (đối đỉnh) => tam giác BIK = CIN (g- c- g)
=> IK = IN mà góc KIN = 60o nên tam giác KIN đều => NK = NI (*)
+) Tam giác ABC cân tại A có góc A = 20 độ => góc ABC = ACB = (180o - 20o)/2 = 80o
+) Xét tam giác BMC có: góc MBC = 80o ; góc BCM = 50o => góc BMC = 50o => tam giác BMC cân tại B => BC = BM mà BC = BI
nên BI = BM => tam giác BMI cân tại B => góc BIM = (180o - MBI) / 2 = 80o
Ta có góc BIC + BIM + MIK = 180o => 60o + 80o + MIK = 180o => góc MIK = 40o
Mà có góc BKC = 180o - (KBC + KCB) = 40o
=> góc MIK = BKC => tam giác MIK cân tại M => MK = MI (**)
từ (*)(**) => NM là đường trung trực của KI Lại có tam giác NIK đều => góc MNI = KNI / 2 = 30o
+) góc BNC = 180o - (NBC + NCB) = 400
Ta có góc MNA + MNI + INC = 180o => MNA + 30o + 40o = 180o => góc MNA = 110o
Vậy....
bằng 110 độ nhé với lại câu hỏi hay đó