Cho bình bình hành AMCN có AB = 8cm , AD = 4cm . Gọi M , N lần lượt là trung điểm của AB và CD a, Chứng minh tứ giác AMNC là hình bình hành . Hỏi tứ giác AMND là hình gì ?b, Gọi I là giao điểm của AN và DM , K là giao điểm của BN và CM . Tứ giác AMND là hình gì ?c, Chứng minh IK song song với CDd, Hình bình hành cần thêm điều kiện gì thì tức giác MINK là gì là hình vuông ? Khi đó , diện tích của MINK bằng...
Đọc tiếp
Cho bình bình hành AMCN có AB = 8cm , AD = 4cm . Gọi M , N lần lượt là trung điểm của AB và CD
a, Chứng minh tứ giác AMNC là hình bình hành . Hỏi tứ giác AMND là hình gì ?
b, Gọi I là giao điểm của AN và DM , K là giao điểm của BN và CM . Tứ giác AMND là hình gì ?
c, Chứng minh IK song song với CD
d, Hình bình hành cần thêm điều kiện gì thì tức giác MINK là gì là hình vuông ? Khi đó , diện tích của MINK bằng bao nhiêu ?
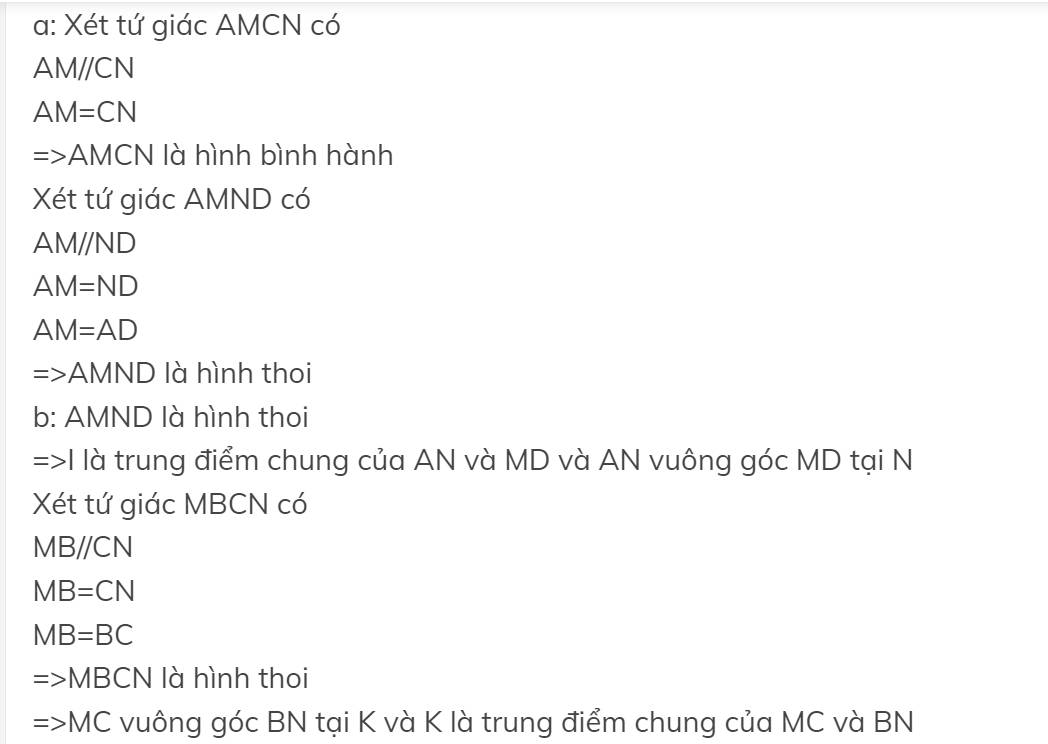
a) Xét tứ giác AMCN có AM // NC ( ABCD là hbh)
AM = NC (gt)
\(\Rightarrow\) AMCN là hbh (dấu hiệu nhận biết)
Xét tứ giác AMND có AM // ND ( ABCD là hình bình hành)
AM = ND (gt)
\(\Rightarrow\) AMND là hbh ( dấu hiệu nhận biết)
c) CMTT : MBCN là hbh có CM cắt BN tại K
\(\Rightarrow\) MK = KC
Hbh AMND có I là giao của AN và DM
\(\Rightarrow\) IM = ID
Xét tam giác MCD có MK = KC (cmt)
IM = ID (cmt)
\(\Rightarrow\) IK là đường trung bình của tam giác MCD ( tính chất của đường trung bình trong tam giác)
\(\Rightarrow\) IK // CD (đpcm)
Xin lỗi bài vừa làm sai rùi tớ sửa lại nha!