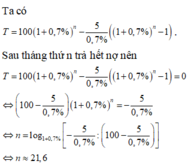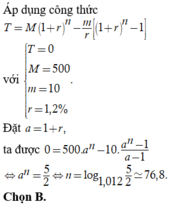Một người vay ngân hàng 40 triệu đồng với lãi suất 0. 85%/ tháng và hợp đồng thỏa thuận là trả 500 ngàn đ mỗi tháng. Sau 1 năm mức lãi suất được điều chỉnh lên là 1. 15%/ tháng và người vay muốn nhanh chóng trả hết nợ nên đã thỏa thuận trả 1 triệu 500 ngàn trên một tháng (trừ tháng cuối). Hỏi phải mất bao lâu thì mới trả dứt nợ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt A=40triệu, d1=500ngàn, d2=1,5triệu; r1=0,85% ; r2=1,15%
Số tiền phải trả còn lại sau 12 tháng đầu tiên là
\(P=A\left(1-r_1\right)^{12}-d_1.\frac{\left(1-r_1\right)^{12}-1}{\left(1-r_1\right)-1}\approx30378140,11\) (đồng)
Gọi x là số tháng hoàn trả hết nợ sau năm thứ nhất
Ta có \(P\left(1-r_2\right)^x-d_2\frac{\left(1-r_2\right)^x-1}{\left(1-r_2\right)-1}=0\)
Giải pt 1ẩn x, ta tìm được \(x\approx18,101\) (sang tháng thứ 19 mới trả hết nợ)
Vậy cần 12+19=31 tháng mới trả hết nợ

Đáp án C
Phương pháp giải: Áp dụng công thức bài toán vay vốn trả góp, hoặc tìm từng tháng, dùng phương pháp quy nạp và đưa về tổng của cấp số nhân
Lời giải:
Sau tháng thứ nhất số tiền gốc còn lại trong ngân hàng là 500(1+0,5%) - 10 triệu đồng.
Sau tháng thứ hai số tiền gốc còn lại trong ngân hàng là
[500(1+0,5%) – 10].(1+0,5%) – 10 = 500.(1+0,5%)2 – 10[(1+0,5%)+1] triệu đồng
Sau tháng thứ ba số tiền gốc còn lại trong ngân hàng là
500.(1+0,5%)3 – 10[(1+0,5%)2 + (1+0,5%) +1] triệu đồng
Số tiền gốc còn lại sau tháng thứ n là
500(2+0,5%)n – 10[(1+0,5%)n-1 + (1+0,5%)n-2 + … + 1] triệu đồng
Đặt y = 1+0,5% = 1,005 thì ta có số tiền gốc còn lại trong ngân hàng sau tháng thứ n là
![]()
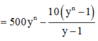
![]()
Vì lúc này số tiền cả gốc lẫn lãi đã trả hết
![]()
![]()
Vậy sau 58 tháng thì người đó trả hết nợ ngân hàng

Đáp án D
Tổng quát:
Giả sử người đó vay ngân hàng số tiền A triệu đồng.
Lãi suất: r % / tháng.
Cuối mỗi tháng người đó trả a triệu đồng.
Cuối tháng đầu tiên, số tiền A triệu đồng ban đầu sinh ra cả gốc lẫn lãi là A + Ar = A 1 + r . Sau khi trả a triệu đồng thì người đó còn nợ A 1 + r − a .
Cuối tháng thứ hai, sau khi trả a triệu đồng người đó còn nợ A 1 + r − a 1 + r − a .
= A 1 + r 2 − a 1 + r − a
…
Cuối tháng thứ n, sau khi trả a triệu đồng người đó còn nợ
A 1 + r n − a 1 + r n − 1 − . .. − a = A 1 + r n − a [ 1 + r n − 1 + 1 + r n − 2 . .. + 1 ]
= A 1 + r n − a . 1 + r n − 1 r
Giả sử đến cuối tháng thứ n thì người đó trả hết nợ, khi đó
A 1 + r n − a . 1 + r n − 1 r = 0
⇔ A 1 + r n = a r 1 + r n − 1 ⇔ 1 + r n a r − A = a r .
Thay số:
n = log 1 + 0 , 6 100 10 10 − 200 . 0 , 6 100 ≈ 21 , 37
Vậy sau ít nhất 22 tháng thì người đó trả được hết số nợ ngân hàng.

Đáp án D
Sau tháng 1: A 1 = 500 1 + 1 , 2 % − 10
Cuối tháng 2: A 2 = A 1 . 1 + 1 , 2 % − 10 = 500 1 + 1 , 2 % 2 − 10 1 + 1 , 2 % − 10
…..
Cuối tháng n:
A n = 500 1 + 1 , 2 % n − 10. 1 + 1 , 2 % n − 1 − ... − 10 = 500 1 + 1 , 2 % n − 10. 1 + 1 , 2 % n − 1 1 + 1 , 2 % − 1 = 0
⇒ 5 + 1 + 1 , 2 % n − 25 3 . 1 + 1 , 2 % n − 1 = 0 ⇒ 10 3 1 + 1 , 2 % n = 25 3 ⇒ n = 77

Tổng số tiền còn nợ ngân hàng sau tháng thứ 1 là ![]()
Tổng số tiền còn nợ ngân hàng sau tháng thứ 2 là
![]()
![]()
Tổng số tiền còn nợ ngân hàng sau tháng thứ n là
![]()
![]()
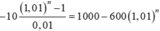
Trước tiên giải ![]()
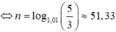
Số tiền còn nợ ngân hàng sau tháng thứ 51 là ![]() đồng.
đồng.
Số tiền phải trả cho ngân hàng cho tháng thứ 52 (kỳ cuối cùng) là
![]() đồng.
đồng.
Chọn đáp án B.