tìm hệ số của x4 y9 trong khai triển (2x-y) 13
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
1
15 tháng 4 2023
Hệ số của x^4 sẽ là tổng của 2*a và 1*b, với a là hệ số của x^3 trong (x-1)^5, b là hệ số của x^4 trong (x-1)^5
SHTQ là: \(C^k_5\cdot x^{5-k}\cdot\left(-1\right)^k=C^k_5\cdot\left(-1\right)^k\cdot x^{5-k}\)
Số hạng chứa x^3 tương ứng với 5-k=3
=>k=2
=>Hệ số là \(C^2_5\cdot\left(-1\right)^2=10\)
Số hạng chứa x^4 tương ứng với 5-k=4
=>k=1
=>Hệ số là \(C^1_5\cdot\left(-1\right)=-5\)
=>Hệ số của x^4 là: 2*10+1*(-5)=20-5=15
ND
1
CM
25 tháng 11 2019
Đáp án A.
Phương pháp:
+) Tổ hợp chập k của n phần tử:
C n k = n ! n − k ! k ! .
+) Công thức khai triển nhị thức Newton:
x + y n = ∑ i = 0 n C n i x i . y n − i .
Cách giải:
5 C n 1 − C n 2 = 5 , n ∈ N , n ≥ 2
⇔ 5 n − n n − 1 2 = 5 ⇔ 10 n − n 2 + n = 0 ⇔ n 2 − 1 ln + 10 = 0 ⇔ n = 10
Khi đó,
2 x + 1 x 2 n = 2 x + x − 2 10 = ∑ i = 0 10 C 10 i 2 x i . x − 2 10 − i = ∑ i = 0 10 C 10 i 2 i x 3 i − 20
Số hạng chứa x 4 trong khai triển ứng với i thỏa mãn
3 i − 20 = 4 ⇔ i = 8
Hệ số a của x 4 trong khai triển:
a = C 10 8 2 8 = 11520.
CM
9 tháng 12 2018
Đáp án A.
Ta có A n 5 ≤ 18 A n - 2 4 ⇔ n ≥ 6 n ! n - 5 ! ≤ 18 . n - 2 ! n - 6 ! ⇔ n ≥ 6 n n - 1 n - 5 ≤ 18 ⇔ 9 ≤ n ≤ 10 → n = 10 .
Với n = 10, xứt khai triển nhị thức
2 x + 1 x x 10 = ∑ k = 10 10 C 10 k . 2 x 10 - k . 1 x 5 x = ∑ k = 0 10 C 10 k . 2 10 - k . x 10 - 6 k 5 .
Hệ số của x 4 ứng với 10 - 6 k 5 = 4 ⇔ k = 5 . Vậy hệ số cần tìm là C 10 5 . 2 5 = 8064 .
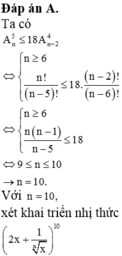
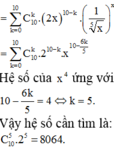
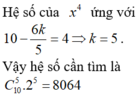
-11440
Ta có: Số hạng bất kì trong khai triển có dạng :
\(T_{k+1}=C^k_{13}.2x^{13-k}.y^k\)
Hệ số của số hạng chứa \(x^4y^9\Leftrightarrow k=9\)
Hệ số : \(T_{10}=C^9_{13}=715\)