- Tìm ba số x,y,z biết rằng chúng tỉ lệ với 3,5,7 và z-y=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CC
1
Những câu hỏi liên quan
L
2
LH
1 tháng 12 2016
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{z-y}{7-5}=\frac{1}{2}\)
Suy ra: \(x=\frac{1}{2}.3=\frac{3}{2};y=\frac{1}{2}.5=\frac{5}{2};z=\frac{1}{2}.7=\frac{7}{2}\)
LH
31 tháng 10 2019
x,y,z tỉ lệ với 3,5,7
suy ra: x/3=y/5=z/7 và z-y=1
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
x/3=y/5=z/7=z-y/7-5=1/2
+) x/3=1/2 suy ra x=3/2
+) y/5=1/2 suy ra y=5/2
+) z/7=1/2 suy ra z=7/2
Vậy x=3/2, y=5/2, z=7/2
HD
2
ZG
6 tháng 11 2017
x/3 =y/5 =z/7 =z−y/7−5 =1/2
Suy ra: x=1/2 .3=3/2 ;y=1/2 .5=5/2 ;z=1/2 .7=7/2
12 tháng 11 2018
Theo đề bài, ta có:
x,y,z tỉ lệ với 3,5,7 => x:y:z=3:5:7
=> x/3=y/5=z/7 và z-y=1
Áp dụng t/c dãy tỷ số bằng nhau, có:
x/3=y/5=z/7=z-y/7-5=1/2
x/3=1/2 => x=3/2
y/5=1/2 => y=5/2
z/7=1/2 => z=7/2
CM
4 tháng 8 2018
Ba số x,y,z tỉ lệ thuận với 3;5;7 nên theo tính chất về tỉ lệ thuận ta có:
x
3
=
y
5
=
z
7
Theo bài ra ta có z - y = 10
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
TH
7
28 tháng 10 2016
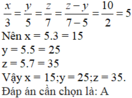
Giải:
Ta có: \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\) và \(x+y+z=180\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{2+3+5}=\frac{180}{10}=18\)
+) \(\frac{x}{2}=18\Rightarrow x=36\)
+) \(\frac{y}{3}=18\Rightarrow y=54\)
+) \(\frac{z}{5}=18\Rightarrow z=90\)
Vậy bộ số \(\left(x,y,z\right)\) là \(\left(36,54,90\right)\)
28 tháng 10 2016
Từ x,y,z tỉ lệ với 2,3,5 => \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{2+3+5}=\frac{180}{10}=18\)
=> \(\begin{cases}x=36\\y=54\\z=90\end{cases}\)
TT
2
DP
19 tháng 5 2019
Vì x,y,z tỉ lệ nghịch với 3,5,7 => \(\frac{x}{\frac{1}{3}}=\frac{y}{\frac{1}{5}}=\frac{z}{\frac{1}{7}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{\frac{1}{3}}=\frac{y}{\frac{1}{5}}=\frac{z}{\frac{1}{7}}=\frac{2x}{\frac{2}{3}}=\frac{y}{\frac{1}{5}}=\frac{3z}{\frac{3}{7}}=\frac{2x-y+3z}{\frac{2}{3}-\frac{1}{5}+\frac{3}{7}}=\frac{68}{\frac{94}{105}}=\frac{3570}{47}\)
\(\frac{2x}{\frac{2}{3}}=\frac{3570}{47}\Rightarrow2x=\frac{2380}{47}\Rightarrow x=\frac{1190}{47}\)
\(\frac{y}{\frac{1}{5}}=\frac{3570}{47}\Rightarrow y=\frac{714}{47}\)
\(\frac{3z}{\frac{3}{7}}=\frac{3570}{47}\Rightarrow3z=\frac{1530}{47}\Rightarrow z=\frac{510}{47}\)
Vậy ....
21 tháng 5 2019
TBRTC:\(3x=5y=7z\Rightarrow\frac{x}{\frac{1}{3}}=\frac{y}{\frac{1}{5}}=\frac{z}{\frac{1}{7}}\)
\(\Rightarrow\frac{2x}{\frac{2}{3}}=\frac{y}{\frac{1}{5}}=\frac{3z}{\frac{3}{7}}\)
Áp dụng t/c
Xong tính x,y,z
25 tháng 2 2022
a: xy=k
nên y=x/k
yz=1
nên \(\dfrac{x}{k}\cdot z=1\)
=>xz=k
Vậy: x tỉ lệ nghịch với z theo hệ số tỉ lệ k
b: xy=k
y=z
nên x/k=z
=>x=kz
Vậy: x tỉ lệ thuận với z theo hệ số tỉ lệ k
c: x=ky
nên y=x/k
yz=1
nên \(\dfrac{xz}{k}=1\)
=>xz=k
Vậy: x tỉ lệ nghịch với z theo hệ số tỉ lệ k
F
3 tháng 11 2017
Theo đề ta có: z = k . y tức là
z = 0,8 . y
y = h . x tức là y = 5 . x
Ta được quyền suy ra:
z = h . k . x => 1/hk . z tức là 5 . 0,8 . x => 1/5 . 0,8 = 1/4
Vậy z tỉ lệ thuận với x
Theo hệ số tỉ lệ 1/hk (hay 1/4)
4 tháng 12 2015
Vì x,y,z tỉ lệ thuận có 3/16;3/6;1/4
nên x/3/16=y/3/6=z/1/4
Áp dụng tính chất dãy tỉ số bằng nhau, ta được: x/3/16=y/3/6=z/1/4=\(\frac{x+y+z}{\frac{3}{16}+\frac{3}{6}+\frac{1}{4}}=\frac{340}{\frac{18}{96}+\frac{48}{96}+\frac{24}{96}}=\frac{340}{\frac{90}{96}}=\frac{1088}{3}\)
Do đó, x=1088/3*3/16=68
y=1088/3*3/6=544/3
z=1088/3*1/4=272/3
Theo đề bài ta có: z-y=1
Và x,y,z tỉ lệ với 3,5,7 suy ra \(x:y:z=3:5:7\Rightarrow\frac{x}{3}=\frac{y}{5}=\frac{z}{7}\)
Áp dụng tc dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{z-y}{7-5}=\frac{1}{2}\)
\(\Rightarrow\begin{cases}\frac{x}{3}=\frac{1}{2}\Rightarrow x=\frac{3\cdot1}{2}=\frac{3}{2}\\\frac{y}{5}=\frac{1}{2}\Rightarrow y=\frac{5\cdot1}{2}=\frac{5}{2}\\\frac{z}{7}=\frac{1}{2}\Rightarrow z=\frac{7\cdot1}{2}=\frac{7}{2}\end{cases}\)