Cho hình chóp đều SABCD có đáy ABCD là hình vuôn có cạnh là 2a , cạnh bên bằng 2a
A) Tính V Khối Chóp
B) Tìm tâm , R của mặt cầu ngoại tiếp khối chóp
C) Tính Smcnt , Vmcnt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 8 2021
\(AC=2a\sqrt{2}.\sqrt{2}=4a\Rightarrow OA=\dfrac{1}{2}AC=2a\)
\(\Rightarrow SO=\sqrt{SA^2-OA^2}=2a\sqrt{3}\)
\(\Rightarrow R=\dfrac{SA^2}{2SO}=\dfrac{4a\sqrt{3}}{3}\)
\(\Rightarrow V=\dfrac{4}{3}\pi R^3=...\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 8 2021
\(AC=2a\sqrt{2}.\sqrt{2}=4a\) \(\Rightarrow OA=\dfrac{1}{2}AC=2a\)
\(\widehat{SAO}=30^0\Rightarrow\left\{{}\begin{matrix}SO=AO.tan30^0=\dfrac{2a\sqrt{3}}{3}\\SA=\dfrac{AO}{cos30^0}=\dfrac{4a\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow R=\dfrac{SA^2}{2SO}=\dfrac{4a\sqrt{3}}{3}\)
\(V=\dfrac{4}{3}\pi R^3=\dfrac{256\pi a^3\sqrt{3}}{27}\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 8 2021
Gọi M là trung điểm AB \(\Rightarrow\widehat{SMO}=45^0\)
\(OM=\dfrac{1}{2}AB=a\sqrt{2}\)
\(SO=OM.tan45^0=a\sqrt{2}\)
\(OA=\dfrac{1}{2}AC=2a\)
\(\Rightarrow SA=\sqrt{SO^2+OA^2}=a\sqrt{6}\)
\(\Rightarrow R=\dfrac{SA^2}{2SO}=\dfrac{3a\sqrt{2}}{2}\)
\(V=\dfrac{4}{3}\pi R^3=9\sqrt{2}\pi a^3\)
CM
15 tháng 10 2017
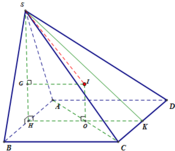
Gọi H là trung điểm của AB, suy ra A H ⊥ A B C D .
Gọi G là trọng tâm tam giác ∆SAB và O là tâm hình vuông ABCD.
Từ G kẻ GI//HO suy ra GI là trục đường tròn ngoại tiếp tam giác ∆SAB và từ O kẻ OI//SH thì OI là trục đường tròn ngoại tiếp hình vuông ABCD.
Ta có hai đường này cùng nằm trong mặt phẳng và cắt nhau tại I.
Suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
R = S I = S G 2 + G I 2 = a 21 6 .
Suy ra thể tích khối cầu ngoại tiếp khối chóp S.ABCD là V = 4 3 π R 3 = 7 21 54 π a 3
Đáp án A
Gọi \(I\) là tâm của đáy \(ABCD\) (giao điểm của \(AC\) và \(BD\))
a) Vì đây là hính chóp đều nên có ngay \(SI\) là đường cao kẻ từ S
\(SI=\sqrt{SA^2-AI^2}=\sqrt{SA^2-\frac{AB^2}{2}}=a\sqrt{2}\)
\(V_{S.ABCD}=\frac{1}{3}.SI.S_{ABCD}=\frac{4a^3\sqrt{2}}{3}\)
b) Thấy ngay \(IA=IB=IC=ID=IS=a\sqrt{2}\)
suy ra tâm mc ngoại tiếp là \(I\) và \(R=a\sqrt{2}\)
c) bạn dùng công thức sau để tính bán kính mặt cầu nội tiếp
\(r=\frac{3V_{S.ABCD}}{S_{ABCD}+4S_{SAB}}=\frac{\frac{4a^3\sqrt{2}}{3}}{4a^2+4.\frac{a^2\sqrt{3}}{2}}=\frac{4\sqrt{2}-2\sqrt{6}}{3}.a\)