Hai ô tô cùng đi từ A đến B. Vận tốc xe thứ nhất bằng 60% vận tốc xe thứ hai. Thời gian xe thứ nhất đi từ A đến B nhiều hơn xe thứ hai là 4 giờ. Tính thời gian đi của mỗi xe
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
27 tháng 11 2018
Gọi thời gian xe thứ nhất đi hết quãng đường AB là a.
Thời gian xe thứ hai đi hết quãng đường AB là b.
\(60\%=\frac{3}{5}\)
Ta có: \(\frac{a}{b}=\frac{5}{3}\Rightarrow\frac{a}{5}=\frac{b}{3}\) và \(a-b=4\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{5}=\frac{b}{3}=\frac{a-b}{5-3}=\frac{4}{2}=2\)
Suy ra:
\(\frac{a}{5}=2\Rightarrow a=10\)
\(\frac{b}{3}=2\Rightarrow b=6\)
CM
19 tháng 11 2018
Gọi v 1 ; v 2 lần lượt là vận tốc của xe thứ nhất và xe thứ hai (km/h) ( v 1 ; v 2 > 0)
Gọi t 1 ; t 2 lần lượt là thời gian của xe thứ nhấy và xe thứ hai (h) ( t 1 ; t 2 > 0)
Từ đề bài ta có: v 1 = 60 100 v 2 ⇒ v 1 = 3 5 v 2 và t 1 = t 2 + 4
Vì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên ta có:
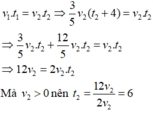
Vậy thời gian người thứ hai đi từ A đến B là 6h
Đáp án cần chọn là B
3 tháng 8 2015
Gọi thời gian xe thứ nhất đi hết quãng đường AB là a
thời gian xe thứ hai đi hết quãng đường AB là b
60% = \(\frac{3}{5}\)
Ta có \(\frac{a}{b}=\frac{5}{3}\Rightarrow\frac{a}{5}=\frac{b}{3}\)
a - b = 4
Áp dụng tính chất dãy tỉ số bằng nhau là
\(\frac{a}{5}=\frac{b}{3}=\frac{a-b}{5-3}=\frac{4}{2}=2\)
Suy ra
\(\frac{a}{5}=2\Rightarrow a=2\cdot5=10\)
\(\frac{b}{3}=2\Rightarrow b=2\cdot3=6\)
Vậy thời gian xe thứ nhất đi hết quãng đường AB là 10 giờ
thời gian xe thứ hai đi hết quãng đường AB là 6 giờ
PM
21 tháng 12 2017
-Gọi thời gian xe 1 là Ta, xe thứ 2 là Tb
-Gọi vận tốc xe 1 là Va, xe 2 là Vb
-Vì đi trên cùng một quãng đường AB nên thời gian và vận tốc là 2 đại lượng tỉ lệ nghịch
-Theo đề bài, ta có:
+ Va . Ta = Vb . Tb
+ Va = 60% Vb
+Tb =Ta-4 hay Tb = Ta-4
Suy ra:
60% Vb . Ta = Vb . Ta-4
Ta -4 =(60% Vb . Ta): Vb
Ta -4 = 3/5 . Ta
Ta - 3/5.Ta = 4
2/5 Ta = 4
Ta = 4 : (2/5)
Ta = 10 (h)
Suy ra,Tb = 10- 4 = 6(h)
Ta có: v1=60% x v2=\(\frac{3}{5}\) x v2
=>\(\frac{v_1}{v_2}\) = \(\frac{3}{5}\)
t1-t2=4h
Vì quãng đường không đổi nên vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.=
\(\frac{v_1}{v_2}\)=\(\frac{t_1}{t_2}\)=> \(\frac{3}{5}\)=\(\frac{t_2}{t_1}\)= \(\frac{t_1}{5}\) = \(\frac{t_2}{3}\) = \(\frac{t_1-t_2}{5-3}\)= \(\frac{4}{2}\)=2.
=> t1= 2 x 5 = 10.
t2= 2 x 3 = 6.
Vậy thời gian đi của xe thứ nhất là 10h.
Thời gian đi của xe thứ hai là 6h.
có được tặng GP không