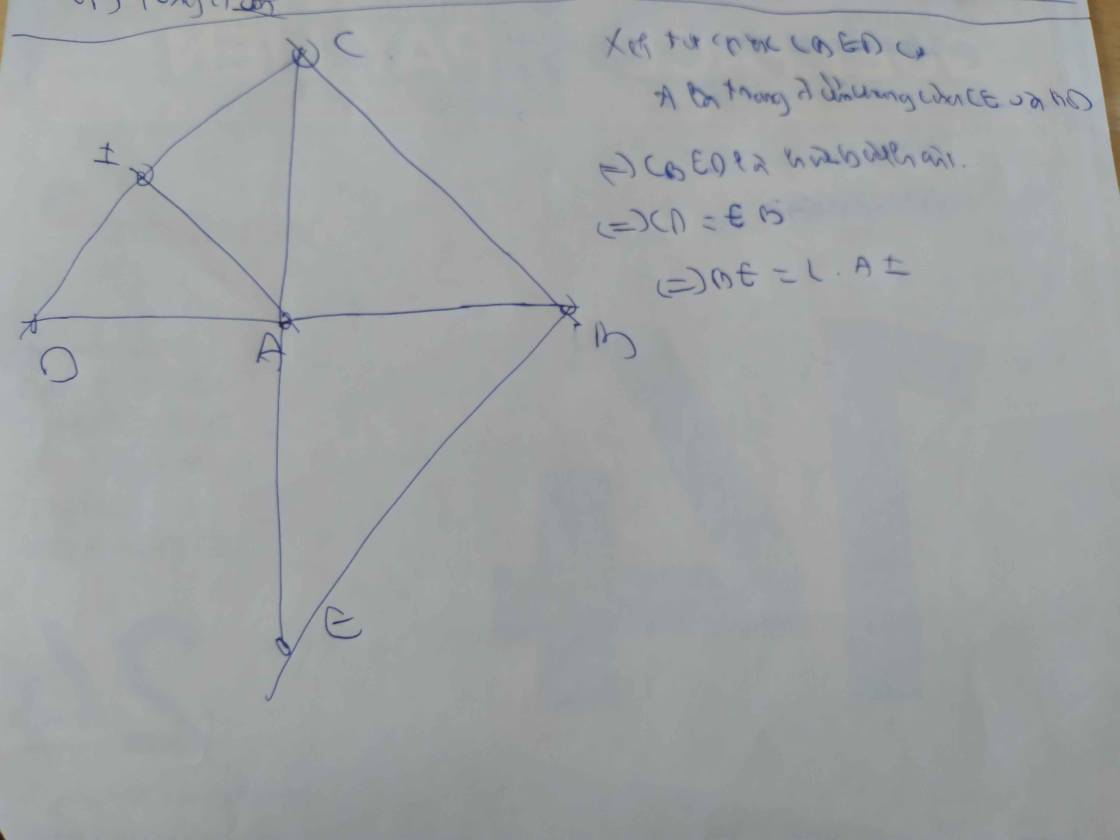
Cho tam giác ABC có góc B và góc C là hai góc nhọn. Trên tia đối cúa tia AB lấy điểm D sao cho AD=AB, trên tia đối của AC lấy E sao cho AE=AC
a) Chứng minh BE=CDb) Lấy M là trung điểm của BE, N là trung điểm của CD. Cm M,A,N thẳng hàngc) Ax là tia bất kì nằm giữa 2 tia AB và AC. Gọi H,K lần lượt là hình chiếu của B và C trên tia Ax. Cm BH + CK < BCd) Xác định vị trí của tia Ax để tổng BH + CK có giá trị lớn nhất CÁC BẠN GIÚP MÌNH PHẦN C với D ĐI ;; ;;Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔADM và ΔACM co
AD=AC
DM=CM
AM chung
=>ΔADM=ΔACM
b: Xét ΔAEN và ΔABN có
AE=AB
EN=BN
AN chung
=>ΔAEN=ΔABN

a: Xét ΔACD có AC=AD
nên ΔACD cân tại A
Xét ΔABE có AB=AE
nên ΔABE cân tại A
b: Xét ΔABC và ΔAED có
AB=AE
\(\widehat{BAC}=\widehat{EAD}\)
AC=AD
Do đó: ΔABC=ΔAED
Suy ra: BC=ED
c: Ta có: ΔABE cân tại A
mà AM là đường trung tuyến
nên AM là đường cao

a) Xét ΔBEAΔBEA và ΔDCAΔDCA có:
AE = AC (gt)
ˆBAE=ˆDACBAE^=DAC^ (đối đỉnh)
AB = AD (gt)
⇒ΔBEA=ΔDCA⇒ΔBEA=ΔDCA (c.g.c)
⇒BE=CD⇒BE=CD (2 cạnh t/ư)
b) Ta có: BM=12BEBM=12BE (M là tđ)
DN=12CDDN=12CD (N là tđ)
mà BE = CD ⇒BM=DN⇒BM=DN
Vì ΔBEA=ΔDCAΔBEA=ΔDCA (câu a)
⇒ˆEBA=ˆCDA⇒EBA^=CDA^ (so le trong)
hay ˆMBA=ˆNDAMBA^=NDA^
Xét ΔABMΔABM và ΔADNΔADN có:
AB = AD (gt)
ˆMBA=ˆNDAMBA^=NDA^ (c/m trên)
BM = DN (c/m trên)
⇒ΔABM=ΔADN(c.g.c)⇒ΔABM=ΔADN(c.g.c)
⇒ˆBAM=ˆDAN⇒BAM^=DAN^ (2 góc t/ư)
mà ˆDAN+ˆNAB=180oDAN^+NAB^=180o (kề bù)
⇒ˆBAM+ˆNAB=180o⇒BAM^+NAB^=180o
⇒M,A,N⇒M,A,N thẳng hàng.

a: Xét ΔEAD và ΔBAC có
AE=AB
\(\widehat{EAD}=\widehat{BAC}\)
AD=AC
Do đó: ΔEAD=ΔBAC
Suy ra: ED=BC
b: Xét ΔACD có AC=AD
nên ΔACD cân tại A
Xét ΔABE có AB=AE
nên ΔABE cân tại A