1 cột đèn cao 4m, bóng của nó trên mặt đất dài 3m. Tính khoảng cách từ đỉnh của cột đèn đến ảnh của nó trên mặt đất? Giải thích.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng định lý pi-ta-go vào tam giác ABI ta có:
\(BI=\sqrt{AB^2+AI^2=}\sqrt{4^2+3^2}\)=5m
Vậy khoảng cách từ đỉnh cột đèn đến bóng của nó trên mặt đất là 5 m

ΔABC vuông tại A có AB=4m; góc B=48 độ. Tính AC
AC=AB*tan48
=4*tan48
\(\simeq4,44\left(m\right)\)

Gọi chân cột đèn là điểm A, đỉnh cột đèn là điểm B và bóng của đỉnh cột trên mặt đất là C
Ta có tam giác ABC vuông tại A với \(AC=7,5\left(m\right)\) và \(\widehat{BCA}=42^0\)
Trong tam giác vuông ABC:
\(AB=AC.tan\widehat{BAC}=7,5.tan42^0\approx6,8\left(m\right)\)

a. Gọi AB là cột điện, A là bóng đèn, A’ là ảnh của bóng đèn qua mặt nước (xem mặt nước như là gương phẳng), các tia tới bất kỳ AI, AK sẽ phản xạ theo hướng A’I và A’K đến mắt (M) của người quan sát
b. Gọi BC là bề rộng của hồ, H là điểm xa nhất mà khi người quan sát đứng tại đó thì mắt của người đó còn nhìn thấy ảnh A’
Nếu người quan sát đi ra ngoài khoảng CH thì mắt không còn nhìn thấy A’ của A qua hồ nữa.
Xét  CBA đồng dạng với
CBA đồng dạng với  CHM
CHM
Ta có:  =
= 

 =
= 
 CH =
CH =  = 4m
= 4m
Vậy khi người ấy rời xa hồ từ 4m trở đi sẽ không còn thấy ảnh của bóng đèn nữa.
mk gặp cùng 1 câu này trên violympic mà sao có lúc ra đ/a là 4, có lúc lại là 12 z các bn

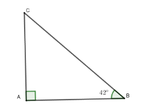
Ta có chiều cao cột đèn là AC; AB = 7,5m và A C B ^ = 42 0
Xét tam giác ACB vuông tại A có:
AC = AB. tan B = 7,5. tan 42 0 ≈ 6,753m
Vậy cột đèn cao 6,753m
Đáp án cần chọn là: A
Áp dụng định lý Py-ta - go => kết quả =5m
5m