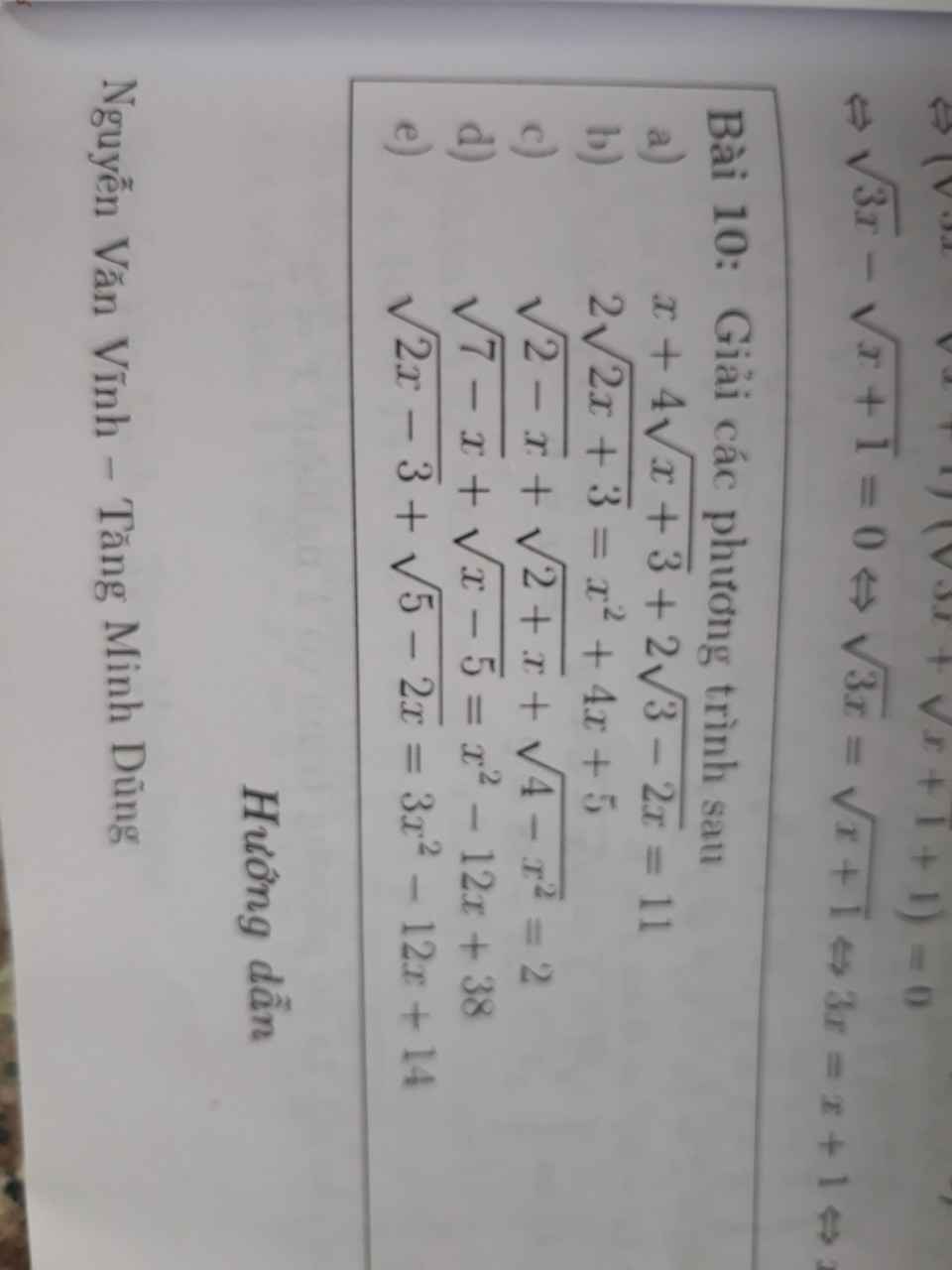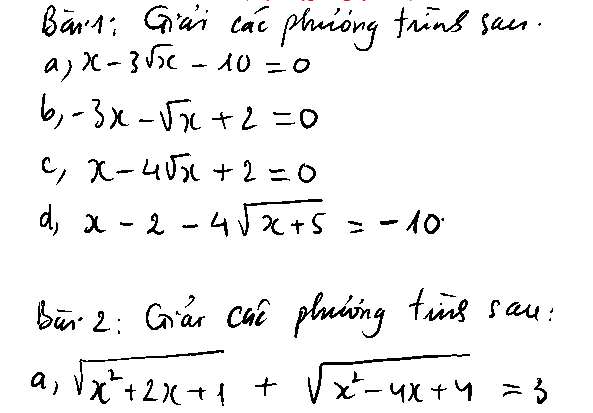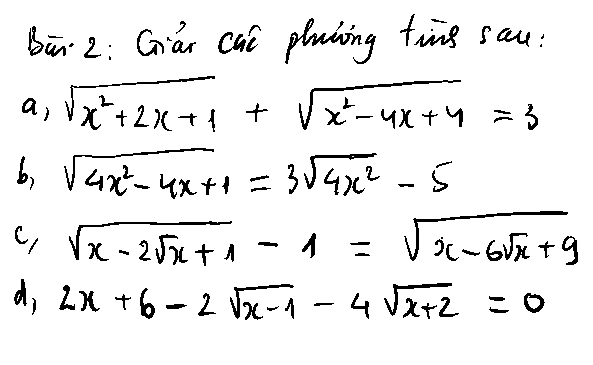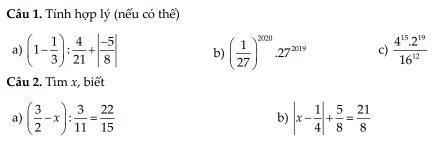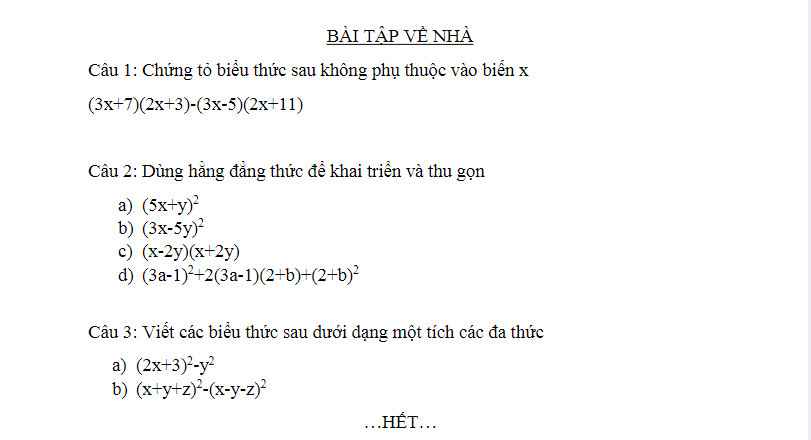Giúp em câu bài a) va bài b)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
a.
ĐKXĐ: \(-3\le x\le\dfrac{3}{2}\)
Ta có:
\(4\sqrt{x+3}=2.2\sqrt{x+3}\le2^2+x+3=x+7\)
\(2\sqrt{3-2x}=2.1.\sqrt{3-2x}\le1^2+3-2x=4-2x\)
Do đó:
\(x+4\sqrt{x+3}+2\sqrt{3-2x}\le x+x+7+4-2x=11\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\sqrt{x+3}=2\\\sqrt{3-2x}=1\end{matrix}\right.\) \(\Leftrightarrow x=1\)
Vậy pt có nghiệm duy nhất \(x=1\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
b.
ĐKXĐ: \(x\ge-\dfrac{3}{2}\)
\(x^2+4x+5-2\sqrt{2x+3}=0\)
\(\Leftrightarrow\left(x^2+2x+1\right)+\left(2x+3-2\sqrt{2x+3}+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2+\left(\sqrt{2x+3}-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=0\\\sqrt{2x+3}-1=0\end{matrix}\right.\)
\(\Leftrightarrow x=-1\)
Vậy pt có nghiệm duy nhất \(x=-1\)
HP
12 tháng 9 2021
1.
d, ĐK: \(x\ge-5\)
\(x-2-4\sqrt{x+5}=-10\)
\(\Leftrightarrow x+5-4\sqrt{x+5}+3=0\)
\(\Leftrightarrow\left(\sqrt{x+5}-1\right)\left(\sqrt{x+5}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=1\\\sqrt{x+5}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=1\\x+5=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
\(\Leftrightarrow x=\pm4\left(tm\right)\)
HP
12 tháng 9 2021
2.
ĐK: \(x\in R\)
\(\sqrt{x^2+2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left|x+1\right|+\left|x-2\right|=3\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\).
\(\left|x+1\right|+\left|x-2\right|=\left|x+1\right|+\left|2-x\right|\ge\left|x+1+2-x\right|=3\)
Đẳng thức xảy ra khi:
\(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Leftrightarrow-1\le x\le2\)
11 tháng 10 2021
\(a,=\dfrac{2}{3}\cdot\dfrac{21}{4}+\dfrac{5}{8}=\dfrac{7}{2}+\dfrac{5}{8}=\dfrac{33}{8}\\ b,=\left(\dfrac{1}{27}\cdot27\right)^{2020}\cdot27=1^{2020}\cdot27=27\\ c,=\dfrac{2^{30}\cdot2^{19}}{2^{48}}=2\)
16 tháng 12 2021
Bài 5:
a: Để đây là hàm số bậc nhất thì m+5<>0
hay m<>-5
26 tháng 9 2021
Câu 1:
Ta có: \(\left(3x+7\right)\left(2x+3\right)-\left(3x-5\right)\left(2x+11\right)\)
\(=6x^2+9x+14x+21-\left(6x^2+33x-10x-55\right)\)
\(=6x^2+23x+21-6x^2-23x+55\)
=76
VT
5
22 tháng 10 2021
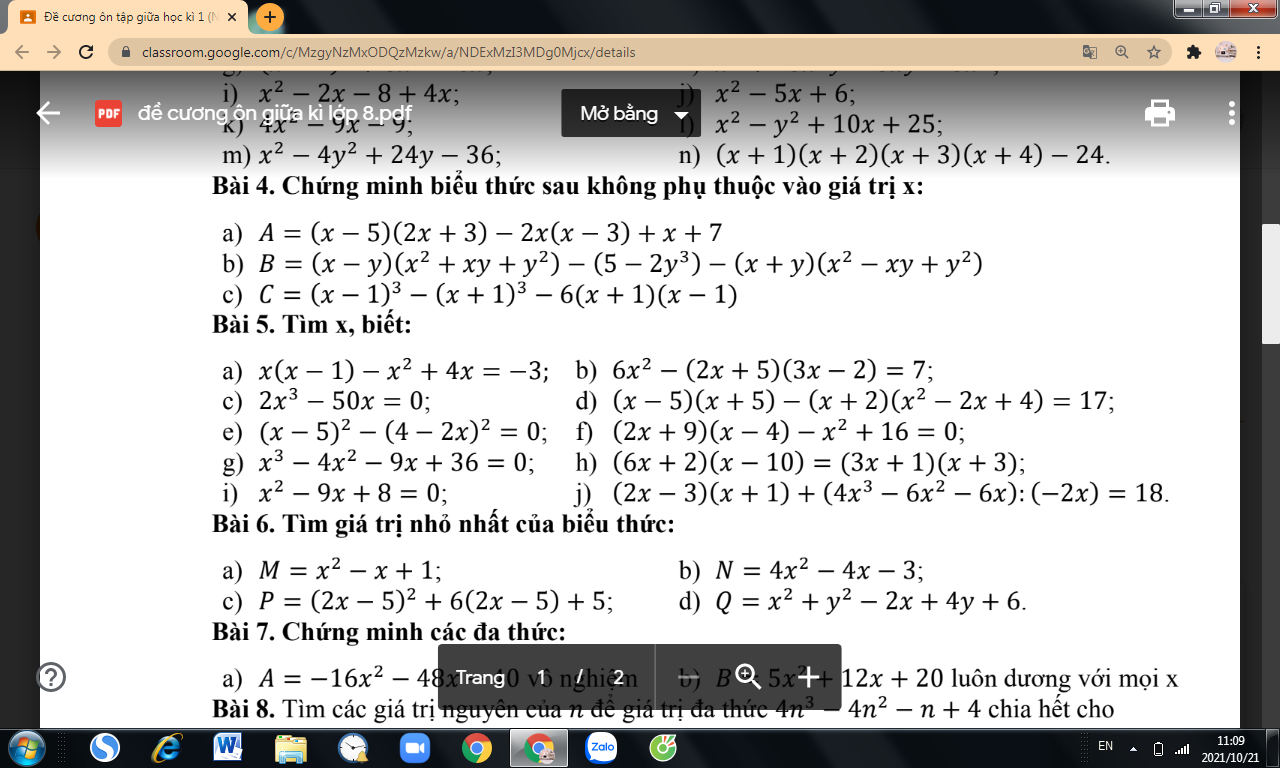
a) \(x\left(x-1\right)-x^2+4x=-3\\ \Rightarrow3x=-3\\ \Rightarrow x=-1\)
b) \(6x^2-\left(2x+5\right)\left(3x-2\right)=7\\ \Rightarrow6x^2-\left(6x^2+15x-4x-10\right)=7\\ \Rightarrow-11x+10=7\\ \Rightarrow x=\dfrac{3}{11}\)
c) \(2x^3-50x=0\\ \Rightarrow2x\left(x^2-50\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x=0\\x^2-50=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=-5\sqrt{2}\\x=5\sqrt{2}\end{matrix}\right.\)
e) \(\left(x-5\right)^2-\left(4-2x\right)^2=0\\ \Rightarrow\left(x-5\right)^2=\left(4-2x\right)^2\\ \Rightarrow\left[{}\begin{matrix}x-5=4-2x\\x-5=2x-4\end{matrix}\right.\\ \Leftarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
f) \(\left(2x+9\right)\left(x-4\right)-x^2+16=0\\ \Rightarrow2x^2+9x-8x-36-x^2+16=0\\ \Rightarrow x^2+x-20=0\\ \Rightarrow\left(x-4\right)\left(x+5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=4\\x=-5\end{matrix}\right.\)