Viết các biểu thức sau đây dưới dạng an (a ϵ Q ; n ϵ N*)
a) 9.35.\(\frac{1}{81}\)
b) 8.24 : \(\left(2^3.\frac{1}{16}\right)\)
c) 32.35:\(\frac{1}{27}\)
d) 125.52.\(\frac{1}{625}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 6:
a: \(2^{27}=8^9\)
\(3^{18}=9^9\)
b: Vì \(8^9< 9^9\)
nên \(2^{27}< 3^{18}\)

a) x2 + 2x + 1
= x2 + 2.x.1 + 12
= (x + 1)2 (Áp dụng hằng đẳng thức (1) với A = x và B = 1)
b) 9x2 + y2 + 6xy
= 9x2 + 6xy + y2
= (3x)2 + 2.3x.y + y2
= (3x + y)2 (Áp dụng hằng đẳng thức (1) với A = 3x và B = y)
c) 25a2 + 4b2 – 20ab
= 25a2 – 20ab + 4b2
= (5a)2 – 2.5a.2b + (2b)2
= (5a – 2b)2 (Áp dụng hằng đẳng thức (2) với A = 5a và B = 2b)
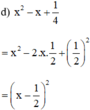
(Áp dụng hằng đẳng thức (2) với A = x và B = 1/2 )

a: Sửa đề: 3^2
\(=3^2\cdot\dfrac{1}{3^5}\cdot3^8\cdot\dfrac{1}{3^3}=3^2\)
b: \(=3^{\left(-2\right)\cdot\left(-2\right)}\cdot\dfrac{1}{3^5}\cdot3^3=\dfrac{3^4}{3^2}=3^2\)
c: \(=2^{12}\cdot2^{16}\cdot2^4=2^{32}\)
d: \(=\left[\dfrac{1}{9}\cdot\dfrac{27}{8}\cdot3\right]\cdot\dfrac{128}{81}\)
\(=\dfrac{16}{9}=\left(\dfrac{4}{3}\right)^2\)

Bài 1:
a) \(4^8\cdot2^{20}=\left(2^2\right)^8\cdot2^{20}=2^{36}\)
\(64^3\cdot4^5=\left(2^6\right)^3\cdot\left(2^2\right)^5=2^{18}\cdot2^{10}=2^{28}\)
\(y\cdot y^7=y^{1+7}=y^8\)
\(a^n\cdot a^2=a^{n+2}\)
Bài 1:
b) \(10^8:2^8=5^8\)
\(17^8:17^5=17^3\)
\(2^{25}:32^4=2^{25}:2^{20}=2^5\)
\(19^4:9^4=\left(\dfrac{19}{9}\right)^4\)
a: \(=3^2\cdot3^5:3^4=3^{2+5-4}=3^3\)
b: \(=2^3\cdot2^4:\left(\dfrac{8}{16}\right)=\dfrac{2^7}{2}=2^6\)
c: \(=3^7\cdot3^3=3^{10}\)
d: \(=5^3\cdot5^2\cdot\dfrac{1}{5^4}=5^1\)