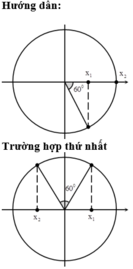
Hai chất điểm dao động điều hòa có cùng T, lệch pha nhau π/3 ,biên độ lần lượt la A và 2A trên 2 trục song song cùng chiều, gốc tọa độ nằm trên đường vuong gốc chung, hai chất điểm chuyển động cùng chiều. Tìm khoảng thời gian ngắn nhất giữa 2 lần chúng đi ngang nhau?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
19 tháng 1 2017
Chọn A.
Giả sử chúng ta gặp nhau ở li độ x1, sau nửa chu kì thì chúng lại gặp nhau ở li độ -x1. Khoảng thời gian hai lần liên tiếp gặp nhau T/2.
VT
9 tháng 4 2019
Đáp án A
Hai vật có li độ ngang nhau khi hình chiếu vị trí của chúng trên trục hoành trùng nhau.
+ Dựa vào giản đồ vecto ta có thể thấy được khoảng thời gian 2 lần liên tiếp chúng trùng nhau là T 2
VT
11 tháng 8 2019
Đáp án A
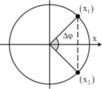
Vòng tròn đơn vị:
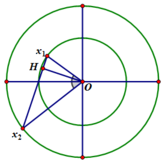
Để 2 vật ngang nhau thì OH phải trùng trục hoành. 2 lần liên tiếp OH trùng trục hoành cách nhau đúng nửa chu kỳ T/2.
VT
25 tháng 3 2017
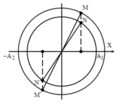
+ Hai vật có li độ ngang nhau khi hình chiếu vị trí của chúng trên trục hoành trùng nhau.
+ Dựa vào giản đồ vecto ta có thể thấy được khoảng thời gian 2 lần liên tiếp chúng trùng nhau là T 2
Đáp án A
VT
8 tháng 5 2017
Đáp án A
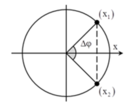
+ Biểu diễn hai vị trí tương ứng trên đường tròn, ta dễ dàng xác định được △ φ = 0 , 5 π
VT
28 tháng 10 2018
Đáp án A
Biểu diễn hai vị trí tương ứng trên đường tròn, ta dễ dàng xác định được △ φ = π 2
VT
24 tháng 2 2017
+ Để mọi thời điểm ba chất điểm luôn thẳng hàng thì: x 2 = x 1 + x 3 2 .
+ Đưa về số phức để bấm máy:
- Chọn MODE 2; SHIFT MODE 4
- Nhập 2 3 ∠ π 6 + 4 ∠ π 2 =
- Kết quả: − 1 2 + 3 2 i
- Chọn SHIFT 2 3 ta được: 1 ∠ 2 π 3
Vậy phương trình vật 2 là: x 2 = c os 4 π t + 2 π 3
ĐÁP ÁN A