tại 2 điểm A và B cách nhau 5cm trong chân không có 2 điện tích q1 = +16\(\times\)10-8 và q2 = \(-\)9\(\times\)10-8 . Tính cường độ điện trường tổng hợp và vẽ vecto cường độ điện trường tại điểm C nằm cách A một khoảng 4cm và cách B một khoảng 3cm .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


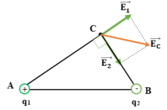
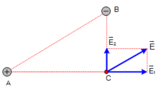
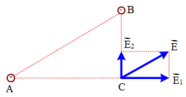
Điện trường do hai điện tích q1 và q2 gây ra tại C được biểu diễn như hình vẽ.
Ta có:
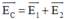
Trong đó:
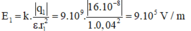
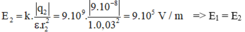
Vì AB = 5cm; AC = 4cm và BC = 3cm
⇒ ΔABC vuông tại C ⇒ 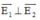
Suy ra 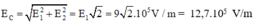
Và EC hợp với cạnh CB một góc 45o.
Đáp số: 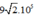 V/m
V/m

đáp án B
E = k . Q r 2 E 1 = 9 . 10 9 . 16 . 10 - 8 0 , 04 2 = 9 . 10 5 E 3 = 9 . 10 9 . 12 . 10 - 8 0 , 03 2 = 12 . 10 5
⇒ E = E 1 2 + E 2 2 = 15 . 10 5 V m

đáp án C

E = k Q r 2 E 1 = 9 . 10 9 . 80 9 0 , 04 2 = 5 . 10 5 E 2 = 9 . 10 9 . 12 . 10 - 8 0 , 03 2 = 12 . 10 5

Có \(BM-AM=AB\Rightarrow M\in AB\) và M nằm ngoài đoạn AB.
\(E_M=\left|E_1-E_2\right|\)
\(E_1=k\dfrac{\left|q_1\right|}{AM^2}=3,6\cdot10^6\)V/m
\(E_2=k\dfrac{\left|q_2\right|}{BM^2}=2\cdot10^6\)V/m
\(\Rightarrow E_M=1,6\cdot10^6V\)/m
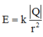
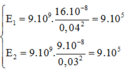
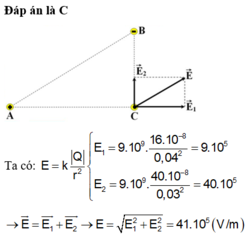
Nhận xét: Do \(AB^2=AC^2+BC^2\) nên tam giác ABC vuông tại C.
Điện trường tổng hợp tại C là: \(\vec{E}=\vec{E_1}+\vec{E_2}\)
Suy ra độ lớn: \(E=\sqrt{E_1^2+E_2^2}\) (*) (do \(\vec{E_1}\) vuông góc với \(\vec{E_2}\) )
\(E_1=9.10^9.\dfrac{16.10^{-8}}{0,04^2}=9.10^5(V/m)\)
\(E_1=9.10^9.\dfrac{9.10^{-8}}{0,03^2}=9.10^5(V/m)\)
Thay vào (*) ta được \(E=9\sqrt2.10^5(V/m)\)
thank you so much