trong 1 bình cách nhiệt chứa 500g nước ở nhiệt độ ban đầu là 10 độ C người ta dùng 1 cái cốc đổ 50g nước vào bình rồi sau khi có cân bằng nhiệt, lại múc ra từ bình 50g nước. Bỏ qua sự trao đổi nhiệt giữa nước với bình, cốc và mt. Các cốc nước đổ vào bình đều có nhiệt độ 60 độ C. Hỏi sau bao nhiêu lượt đổ và múc thì nhiệt độ nước > 55 độ C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
21 tháng 8 2019
Đáp án : A
- Gọi m 1 ; m 2 là lượng nước có trong bình 1, bình 2 lúc ban đầu.
- Khi đổ một lượng nước 0,05(kg) từ bình 2 sang bình 1. nước ở bình 1 có nhiệt độ cân bằng là 35 0 C .
- Ta có:
m 1 .c.(35 - 30) = 0,05.c.(60 - 35)
- Hay:
m 1 .5 = 0,05.25 ⇒ m 1 = 0,25 (kg)
- Sau khi đổ 0,05 (kg) từ bình 1 sang bình 2 thì nhiệt độ ở bình 2 sau khi cân bằng là 50 0 C ta lại có:
( m 2 – 0,05).c.(60 - 50) = 0,05.c(50 - 35)
⇒( m 2 – 0,05).10 = 0,05.15 ⇒ m 2 = 0,125 (kg)
4 tháng 10 2023
Gọi \(m\left(kg\right)\) là khối lượng nước bình 1 và bình 2 ban đầu.
Và \(m'\left(kg\right)\) là lượng nước được múc ra.
Khi bình 2 cân băng nhiệt, người ta múc một ca nước từ bình 2 đổ sang bình 1 và nhiệt độ bình 1 khi cân bằng nhiệt là 30. Ta có pt:
\(m\cdot c\cdot\left(30-20\right)=m'\cdot c\cdot\left(60-30\right)\Rightarrow10m=30m'\Rightarrow m=3m'\)
Nếu lặp lại một lần nữa, nhiệt độ bình 1 sau khi cân bằng là \(t\left(^oC\right):\)
\(\left(m-m'\right)\cdot c\cdot\left(60-t\right)=m'\cdot c\cdot\left(t-20\right)\)
\(\Rightarrow2\cdot\left(60-t\right)=t-20\Rightarrow t=\dfrac{140}{3}\approx46,67^oC\)
MN
17 tháng 2 2021
nếu sửa đề :
có hai bình cách nhiệt đủ lớn cùng đựng 1 lượng nước ,ở bình 1 nhiệt độ t1, bình 2 t2.Lúc đầu người ta rót 1 nửa lượng nước từ bình 1 sang bình 2. Khi thấy cân bằng nhiệt thì thấy nhiệt độ nước trong bình 2 tăng gấp đôi nhiệt độ ban đầu. Sau đó người ta lại rót 1 nửa lượng nước đang có từ bình 2 sang bình 1. Nhiệt độ trong bình 1 sau khi đã CBN là 30oC (bỏ qua sự trao đổi nhiệt giữa mtrường)
a) Tính t1,t2
b) Nếu rót hết phần nước còn lại từ bình 2 sang bình 1 thì nhiệt đọ bình 1 khi đã cân bằng nhiệt là bao nhiêu ?
Lời giải :
Nguồn : https://h.o.c.24.vn/cau-hoi/co-hai-binh-cach-nhiet-du-lon-dung-cung-mot-luong-nuoc-binh-1-o-nhiet-do-t1-va-binh-2-o-nhiet-do-t2-luc-dau-nguoi-ta-rot-mot-nua-luong-nuoc-trong.260789230992
nếu không xem đc hình thì vào tkhđ
MN
17 tháng 2 2021
j dzay olm lag a , vô link cung dc
Có hai bình cách nhiệt đủ lớn, đựng cùng một lượng nước, bình 1 ở nhiệt độ t1 và bình 2 ở nhiệt độ t2. Lúc đầu người ta... - H.o.c24
LU
20 tháng 3 2016
Gọi nhiệt độ bình 2 sau khi đã cân bằng nhiệt là t1 (\(^oC\)):
- Phương trình cân bằng nhiệt sau sau khi rót lần 1:
\(m.C\left(80-t_1\right)=2.C\left(t_1-20\right)\) (1)
- Phương trình cân bằng nhiệt sau sau khi rót lần 2:
\(\left(4-m\right).C.\left(80-74\right)=m.C\left(74-t_1\right)\) (2)
Đơn giản C ở 2 vế các phương trình (1) và (2)
Giải hệ phương trình gồm (1) và (2)
\(\begin{cases}m\left(80-t_1\right)=2.\left(t_1-20\right)\\\left(4-m\right).6=m\left(74-t_1\right)\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}80m-mt_1=2t_1-40\\24-6m=74m-mt_1\end{cases}\)\(\Rightarrow\)\(\begin{cases}80m=2t_1+mt_1-40\\80m=mt_1+24\end{cases}\)
\(\Rightarrow2t_1=\) 24 + 40 = 64 \(\Rightarrow t_1=\) 32
Thay \(t_1\) = 32 vào (1) ta có : m( 80 - 32) = 2 ( 32 - 20) \(\Rightarrow\) m.48 = 2.12 = 24
\(\Rightarrow\) m = 24:48 = 0,5 (kg)
Vậy : Khối lượng nước đã rót mỗi lần là m = 0,5 (kg)
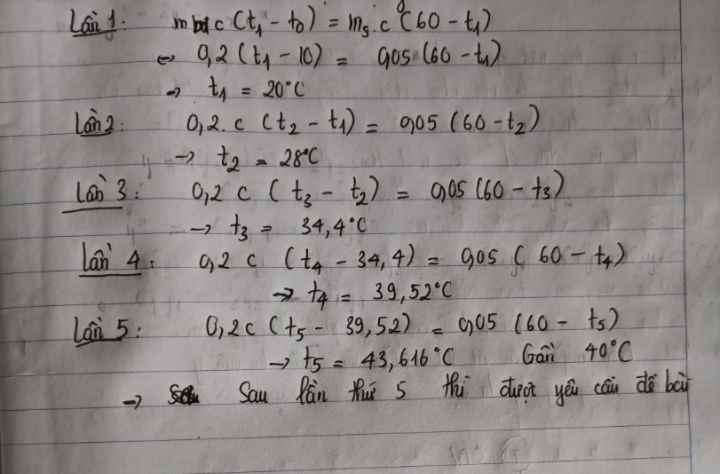
Đổi: \(500g=0,5kg,50g=0,05kg\)
Nhiệt lượng nước thu vào để đạt đến \(55^0C\) là :
\(Q_{thu}=m_n.c_n.\Delta t=94500\left(J\right)\)
Giả sử ta đổ cùng một lúc một khối nước có khối lượng gồm n cốc vào bình.
\(\Rightarrow\) Khối lượng khối nước đó là : \(m=n.0,05\)
\(\Rightarrow\)Nhiệt lượng mà khối nước tỏa ra là: \(Q=m.c_n.\Delta t=n.0,05.4200.5=1050.n\left(J\right)\)
\(\Rightarrow1050.n=94500\)
\(\Rightarrow n=90\)
Vậy ta cần đổ - múc tối thiểu 90 lượt thì sẽ được nước có yêu cầu như đề bài!!
Đâu phải nhiệt toả ra của mỗi cốc nước nước luôn bằng nhau trong mỗi lượt đâu mà bạn chia