Con lắc đơn có chiều dài l=1m. Đặt tại nơi có g=10m/s2, chọn gốc thế năng tại vị trí cân bằng. Con lắc dao động với biên độ α0=8o. Giá trị vận tốc của vật tại vị trí mà ở đó động năng bằng thế năng là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



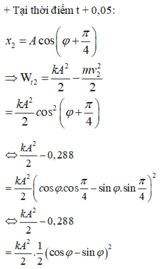


Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác:

Đáp án D

Đáp án D
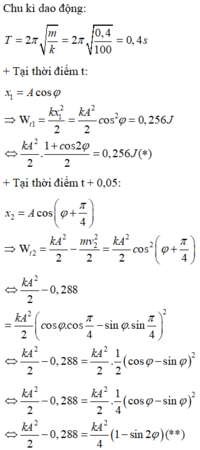
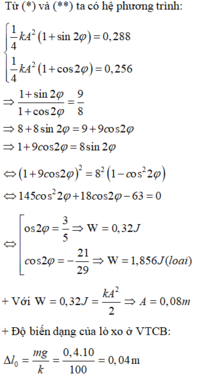
+ Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác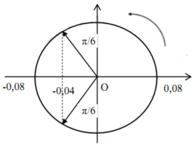
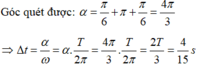

Chọn đáp án B
+ Tần số dao động con lắc đơn: f = ω 2 π = 1 2 π g l

Bạn áp dụng CT của dao động điều hòa:
\(A^2=x^2+\dfrac{v^2}{\omega^2}\)
Với \(x=\alpha.\ell\), li độ là độ dài cung của góc \(\alpha\) (tính theo rad)
\(\Rightarrow (\alpha_0.\ell)^2=(\alpha.\ell)^2+\dfrac{v^2.\ell}{g}\)
\(\Rightarrow \alpha_0^2=\alpha^2+\dfrac{v^2}{g\ell}\)
Chọn đáp án A.

Chọn mốc thế năng ở mặt đất.
a) Cơ năng ban đầu của vật: \(W_1=m.g.h_1=0,5.10.100=500(J)\)
Tại độ cao h2 = 50m thì thế năng là: \(W_{t2}=m.gh_2=0,5.10.50=250(J)\)
Cơ năng tại vị trí này: \(W_2=W_{đ2}+W_{t2}\)
Áp dụng định luật bảo toàn cơ năng ta có: \(W_2=W_1=500(J) \Rightarrow W_{đ2}=500-250=250(J)\)
b) Tại vị trí động năng bằng thế năng:
\(W_đ=W_t\Rightarrow W=2.W_t\Rightarrow m.g.h_1=2.m.g.h_3\)
\(\Rightarrow h_3=\dfrac{h_1}{2}=\dfrac{100}{2}=50(m)\)

Chọn D.
Bỏ qua sức cản không khí nên cơ năng được bảo toàn
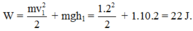

Đáp án D
Phương pháp: Thế năng đàn hồi:
Cách giải:
Độ dãn của lò xo tại vị trí cân bằng: Δ l 0 = m g k = 0,2.10 80 = 0,025 m = 2,5 c m
Biên độ dao động của con lắc: A = 7 , 5 - Δ l 0 = 7 , 5 - 2 , 5 = 5 c m
Ta có: Δ l 0 < A
Chọn chiều dương hướng xuống
⇒ Vị trí lực đàn hồi có độ lớn nhỏ nhất là vị trí lò xo không giãn cũng không nén: Δ l = 0
Thế năng đàn hồi tại vị trí đó: W t = 1 2 k Δ l 2 = 1 2 80. ( 0 ) 2 = 0 J

Do \(\alpha_0=8^0\) nên đây là dao động điều hòa, ta tính toán giống như một dao động điều hòa thôi.
Tại vị trí \(W_đ=W_t\)
\(\Rightarrow W=W_đ+W_t=2W_đ\)
\(\Rightarrow v_{max}^2=2.v^2\)
\(\Rightarrow v=\dfrac{v_{max}}{\sqrt 2}=\dfrac{\omega.A}{\sqrt 2}\)
\(\Rightarrow v=\dfrac{\sqrt{\dfrac{g}{\ell}}.\alpha_0.\ell}{\sqrt 2}=\dfrac{\alpha_0.\sqrt{g.\ell}}{\sqrt 2}\)
\(\Rightarrow v=\dfrac{\dfrac{8.\pi}{180}.\sqrt{10.1}}{\sqrt 2}\approx0,31(m/s)\)
Cảm ơn bạn