Xác định hàm số f(x) biết f(x+1)=x^2-3x+2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Hướng dẫn: Đặt: \(X=\frac{3x+1}{x+2}\)
=> \(X=\frac{3x+1}{x+2}=\frac{3x+6-5}{x+2}=3-\frac{5}{x+2}\)
=> \(\frac{5}{x+2}=3-X\Rightarrow x=\frac{5}{3-X}-2\)
=> \(f\left(X\right)=\frac{\frac{5}{3-X}-2}{\frac{5}{3-X}-1}=\frac{2X-1}{X+2}\)
Vậy hàm số f(x) có dạng: \(f\left(x\right)=\frac{2x-1}{x+2}\)
p/s: chú ý điều kiện

Chọn C.
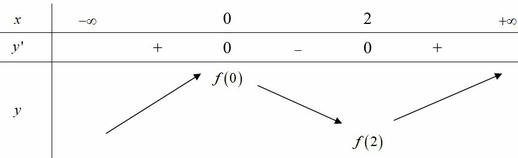
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.

a: f(x)=3x^2
a=3>0
=>Hàm số đồng biến khi x>0 và nghịch biến khi x<0
b: f(1)=f(-1)=3*1^2=3
f(2)=3*2^2=12
f(-4)=3*(-4)^2=48
c: f(x)=48
=>x^2=48/3=16
=>x=4 hoặc x=-4
d; 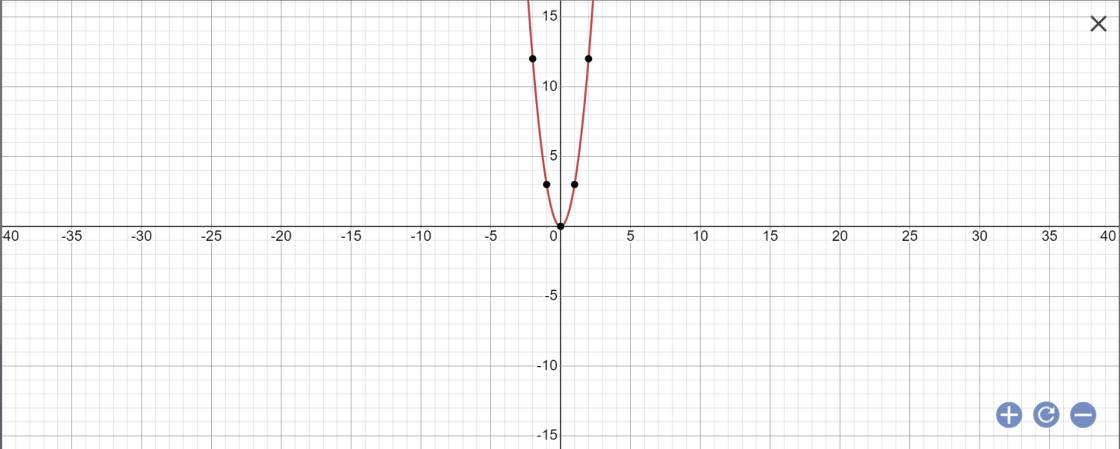

a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)


a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)




Thấy f(x) = f [ (x-1) +1 ] = (x+1)^2 -3(x+1) + 3 = x^2 -x -2
Đặt \(x+1=t\Rightarrow x=t-1\)
\(f\left(t\right)=\left(t-1\right)^2-2\left(t-1\right)+3=t^2-2t+1-2t+2+3=t^2-4t+6\)
Vậy \(f\left(x\right)=x^2-4x+6\)