Một vật dao động điều hòa với phương trình (\(x =4cos(\omega t-\pi/3)cm.\)Trong giây đầu tiên vật đi được quãng đường là 6cm. Trong giây thứ 2013 vật đi được quãng đường là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


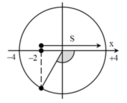
+ Biểu diễn dao động của vật tương ứng trên đường tròn.
+ Tại t = 0 , vật đi qua vị trí x = -0,5A = -2 cm theo chiều dương.
→ Sau khoảng thời gian 1 s, vật đi được quãng đường S = 0,5A+A = 6 cm → Vật đến biên.
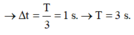
Ta chú ý rằng, sau khoảng thời gian 2016 s = 672 T vật quay về vị trí ban đầu → trong 1 s thứ 2017 vật cũng sẽ đi được quãng đường 6 cm.
Đáp án A

Đáp án A
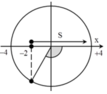
+ Biểu diễn dao động của vật tương ứng trên đường tròn
+Tại t=0,vật đi qua vị trí x=-0,5 A=-2cm theo chiều dương
->Sau khoảng thời gian 1 s, vật đi được quãng đường S = 0 , 5 A + A = 6 c m
Vật đến biên → Δ t = T 3 = 1 s . → T = 3 s .
+ Ta chú ý rằng, sau khoảng thời gian 2016 s = 672 T vật quay về vị trí ban đầu -> trong 1 s thứ 2017 vật cũng sẽ đi được quãng đường 6 cm

Đáp án A

+ Biểu diễn dao động của vật tương ứng trên đường tròn.
+ Tại t=0, vật đi qua vị trí x=-0,5 A=-2cm theo chiều dương
-> Sau khoảng thời gian 1 s, vật đi được quãng đường S=0,5A+A=6cm->Vật đến biên
→ Δ t = T 3 = 1 s . → T = 3 s .
+ Ta chú ý rằng, sau khoảng thời gian 2016 s = 672 T vật quay về vị trí ban đầu -> trong 1 s thứ 2017 vật cũng sẽ đi được quãng đường 6 cm

Trong giây thứ 2019 thiệt à?
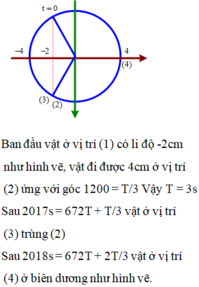
Vậy thì khó gì, vẽ đường tròn ra và phân tích thôi
\(T=\dfrac{2\pi}{\pi}=2\left(s\right)\) => 1s nó đi được 4+4=8 (cm)
Trong khoảng thời gian từ t=0 đến t=2018 thì vật đi được 2018/2=1009 chu kỳ và trở lại vị trí ban đầu=> Đi được 8(cm)


\(20-10\sqrt{2\left(A-\frac{A}{\sqrt{2}}\right)}\Rightarrow\frac{T}{4}=1\Rightarrow T=4\left(s\right)\)
\(S=S_{2012}-S_{2011}=A\sqrt{2}=10\sqrt{2}\) (cm)
Không có đáp án đó nhưng bạn giải thích cách làm của bạn cho mình với.