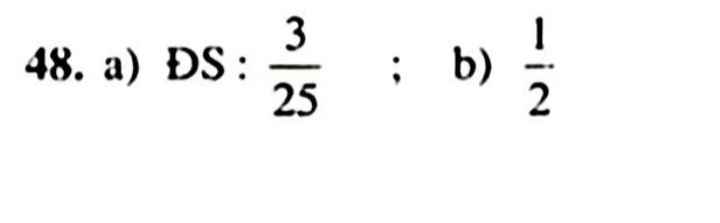K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1
17 tháng 7 2016
\(\frac{3^6.\left(3^2.5\right)^4-\left(3.5\right)^3:5^9}{\left(3^3\right)^4.\left(5^2\right)^3+\left(5.3^2\right)^6}\) = \(\frac{3^{14}.5^4-3^3:5^6}{3^{12}.5^6+5^6.3^{12}}\) = \(\frac{3^{14}.5^{10}-3^3}{3^{12}.5^{12}+5^{12}.3^{ }^{12}^{ }}=\frac{3^{11}.5^{10}-1}{2.3^9.5^{12}}\)
DT
1
10 tháng 8 2023
\(\dfrac{3^6.45^4-15^{13}.5^{-9}}{27^4.25^3+45^6}=\dfrac{3^6.3^85^4-3^{13}.5^{13}.5^{-9}}{3^{12}.5^6+3^{12}.5^6}\)
\(=\dfrac{3^{14}.5^4-3^{13}.5^4}{2.3^{12}.5^6}=\dfrac{3^{13}.5^4\left(3-1\right)}{2.3^{12}.5^6}\)
\(=\dfrac{3.2}{2.5^2}=\dfrac{3}{25}\)
LQ
0
TQ
1
10 tháng 9 2017
\(\frac{3^6.45^4-15^{13}:5^9}{27^4.25^3+45^6}\)=\(\frac{3^{14}.5^4-3^{13}.5^4}{3^{12}.5^6+3^{12}.5^6}=\frac{3^{13}.5^4\left(3-1\right)}{3^{12}.5^6\left(1+1\right)}\)=\(\frac{3}{25}\)
RT
1
8 tháng 8 2016
\(E=\frac{3^6.45^4-15^{13}.5^{-9}}{27^4.25^3+45^6}\)
\(E=\frac{3^6.3^8.5^4-3^{13}.5^{13}.5^{-9}}{3^{12}.5^6+3^{12}.5^6}\)
\(E=\frac{3^{14}.5^4-3^{13}.5^4}{3^{12}.5^6\left(1+1\right)}\)
\(E=\frac{3^{13}.5^4\left(3-1\right)}{3^{12}.5^6.2}\)
\(E=\frac{3}{25}\)
DH
16
13 tháng 9 2021
\(a,=\dfrac{3^6\cdot5^4\cdot9^4-5^{13}\cdot3^{13}\cdot5^{-9}}{3^{12}\cdot5^6+9^6\cdot5^6}=\dfrac{3^{14}\cdot5^4-5^4\cdot3^{13}}{3^{12}\cdot5^6+3^{12}\cdot5^6}\\ =\dfrac{3^{13}\cdot5^4\cdot2}{2\cdot3^{12}\cdot5^6}=\dfrac{3}{5^2}=\dfrac{3}{25}\)
13 tháng 9 2021
\(b,=\dfrac{\left(\dfrac{2}{5}\cdot5\right)^7+\left(\dfrac{9}{4}\cdot\dfrac{16}{3}\right)^3}{2^7\cdot5^2+2^9}=\dfrac{2^7+12^3}{2^7\left(5^2+2^2\right)}=\dfrac{2^7+4^3\cdot3^3}{2^7\cdot29}=\dfrac{2^6\left(2+3^3\right)}{2^7\cdot29}=\dfrac{1}{2}\)
TP
1
24 tháng 5 2022
\(=\dfrac{3^6\cdot\left(3^2\right)^4\cdot5^4-5^{13}\cdot3^{13}\cdot5^{-9}}{3^{12}\cdot5^6+\left(3^2\right)^6\cdot5^6}\)
\(=\dfrac{3^{14}\cdot5^4-5^4\cdot3^{13}}{3^{12}\cdot5^6+3^{12}\cdot5^6}=\dfrac{3^{13}\cdot5^4\cdot2}{2\cdot3^{12}\cdot5^6}=\dfrac{3}{5^2}=\dfrac{3}{25}\)