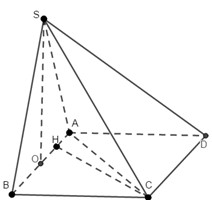
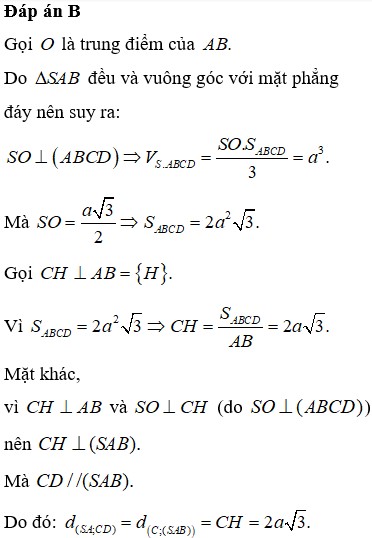Cho hình chóp sabcd có đáy là hcn ac= 2a. Biết tam giác sab đều cạnh a và nằm trong mp vuông góc vs mp abcd. Tính thể tích khối chóp và tính độ dài đoạn MN với M ,N trung đieemr SA và BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 7 2018
Gọi M là trung điểm cạnh AB
Dựa vào tính chất hai mặt phẳng vuông góc với nhau suy ra SM⊥(ABC)
⇒ V S.ABC = 1/3.SΔABC.SM = 1/3.1/2.AC.BC.SM
Gọi N là trung điểm của đoạn AC
MN là đường trung bình của tam giác ABC
⇒ MN ⊥ AC; MN = 1/2.BC = a
Chỉ ra góc giữa mặt phẳng (ABC) và mặt phẳng (SAC) là SMN=60 độ
Tính thể tích hình chóp S.ABC
SM = MN.tanSNM = a.tan60 = a√3.
SN = MN/cosSNM = a/cos60 = 2a.
AB = 2SM = 2a√3.
AC = √(AB^2 − BC^2) = √[(2a√3)^2−(2a)^2]=2a√2
Vậy V S.ABC = 1/3.SΔABC.SM = 1/3.1/2.AC.BC.SM = (2a^3√6)/3 (đvtt)
CM
6 tháng 12 2017
Phương pháp:
Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: V = 1 3 S h
Cách giải:
CM
15 tháng 10 2017
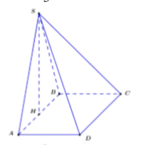
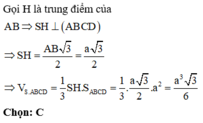
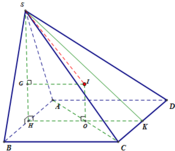
Gọi H là trung điểm của AB, suy ra A H ⊥ A B C D .
Gọi G là trọng tâm tam giác ∆SAB và O là tâm hình vuông ABCD.
Từ G kẻ GI//HO suy ra GI là trục đường tròn ngoại tiếp tam giác ∆SAB và từ O kẻ OI//SH thì OI là trục đường tròn ngoại tiếp hình vuông ABCD.
Ta có hai đường này cùng nằm trong mặt phẳng và cắt nhau tại I.
Suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
R = S I = S G 2 + G I 2 = a 21 6 .
Suy ra thể tích khối cầu ngoại tiếp khối chóp S.ABCD là V = 4 3 π R 3 = 7 21 54 π a 3
Đáp án A
CM
18 tháng 10 2018
Đáp án là A.
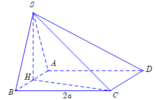
V S . A B C D = 4 a 3 3 = 1 3 .4 a 2 . S H
S C = S H 2 + H C 2 = S H 2 + B H 2 + B C 2 = a 6 .