cho tập A= { 0;1;2;3;4;5} lập số tự nhiên có 3 chữ số đôi một khác nhau.chọn ngẫu nhiên 2 số trong các số vừa lập ,tinh xác suất để trong hai số được chọn có đúng một số chẵn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
1 tháng 4 2020
cho tập hợp A = { -3 ;-2 ; 0 ; 6 ; 9 }. trong các 1 tập hợp sau tập hợp nào ko phải là tập hợp con của A ?
A. {-3 , 9} B. {-2 , 0 , -9 } C. {-3 ,0 , 6 ,9 } D . {-2}
CM
28 tháng 11 2019
a, x – 9 = 13 => x = 13 + 9 => x = 22
Vậy M = {22} và M có 1 phần tử
b, x + 6 = 34
x = 34 – 6
x = 28
Vậy H = {28} và H có 1 phần tử.
c, x.0 = 0 luôn đúng với mọi x ∈ N
Vậy O = N và O có vô số phần tử
d, a) x.0 = 3 không thỏa mãn vì trong tập hợp các số tự nhiên, số nào nhân với 0 cũng bằng 0
Vậy A = { ∅ } và A có 0 phần tử
e, (x – 2)(x – 5) = 0
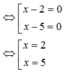
Vậy N = {2;5} và N có 2 phần tử
f, a) x : 0 = 0 không có số tự nhiên nào thỏa mãn vì không thể chia cho 0
Vậy G = { ∅ } và G có 0 phần tử
LB
1 tháng 10 2023
Tập hợp A là : {3;6;9;12;15;18;21;24;27}
Tập hợp B là : {9;18;27}
25 tháng 8 2023
a: A={x\(\in R\)|x^2+x-6=0 hoặc 3x^2-10x+8=0}
=>x^2+x-6=0 hoặc 3x^2-10x+8=0
=>(x+3)(x-2)=0 hoặc (x-2)(3x-4)=0
=>\(x\in\left\{-3;2;\dfrac{4}{3}\right\}\)
=>A={-3;2;4/3}
B={x\(\in\)R|x^2-2x-2=0 hoặc 2x^2-7x+6=0}
=>x^2-2x-2=0 hoặc 2x^2-7x+6=0
=>\(x\in\left\{1+\sqrt{3};1-\sqrt{3};2;\dfrac{3}{2}\right\}\)
=>\(B=\left\{1+\sqrt{3};1-\sqrt{3};2;\dfrac{3}{2}\right\}\)
A={-3;2;4/3}
b: \(B\subset X;X\subset A\)
=>\(B\subset A\)(vô lý)
Vậy: KHông có tập hợp X thỏa mãn đề bài
- Có 5 cách chọn chữ số hàng trăm.
- Có 5 cách chọn chữ số hàng chục.
- Có 4 cách chọn chữ số hàng đơn vị.
Số số được tạo thành là:
\(5.5.4=100\) (số)
Tuy nhiên trong 100 số này đã bị mất đi 1 số số chẵn:
Vậy số số lẻ hơn số số chẵn là 8 số.
Có số số chẵn là:
\(\left(100-8\right):2=46\) (số)
Có số số lẻ là :
\(100-46=54\) (số)
Nếu coi 100 số là 100 %.
Xác xuất chọn được số chẵn ở lần chọn đầu là:
\(46:100.100=46\%\)
Xác xuất chọn được số chẵn ở lần chọn thứ 2 (nếu lần ko trúng) là:
\(46:99.100\approx46,5\)