3 Một cây cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc của tia sáng mặt trời tạo với mặt đất.
4 Cho DABC có đường cao AH. Biết AB = 25 cm, , . Tính độ dài AH và BC (làm tròn đến chữ số thập phân thứ hai)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

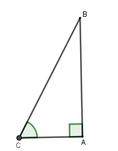
Ta có: tan C = A B A C = 7 4 ⇒ C ^ ≃ 60 0 15 '
Đáp án cần chọn là: D

Kí hiệu như hình vẽ. Theo hệ thức giữa các cạnh và góc của tam giác vuông, ta có:
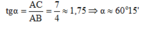

Kí hiệu như hình vẽ. Theo hệ thức giữa các cạnh và góc của tam giác vuông, ta có:

Bài 2
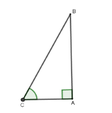
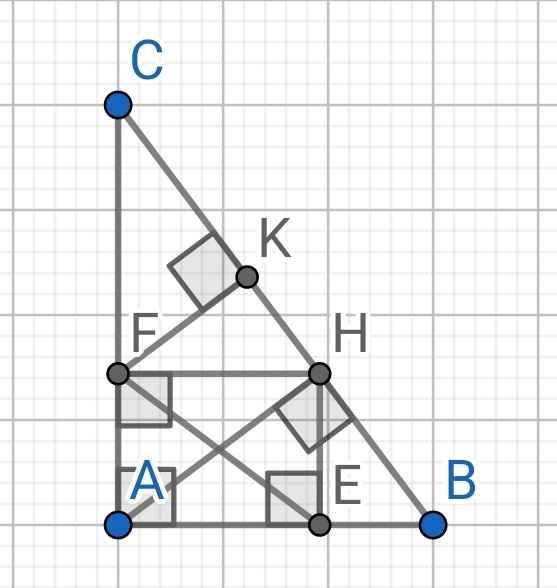 a) ∆ABC vuông tại A, AH là đường cao
a) ∆ABC vuông tại A, AH là đường cao
⇒ AH² = BH.HC
= 4.9
= 36
⇒ AH = 6 (cm)
BC = BH + HC
= 4 + 9 = 13 (cm)
∆ABC vuông tại A, AH là đường cao
⇒ AB² = BH.BC
= 4.13
= 52 (cm)
⇒ AB = 2√13 (cm)
⇒ cos ABC = AB/BC
= 2√13/13
⇒ ∠ABC ≈ 56⁰
b) ∆AHB vuông tại H, HE là đường cao
⇒ AH² = AE.AB (1)
∆AHC vuông tại H, HF là đường cao
⇒ AH² = AF.AC (2)
Từ (1) và (2) suy ra:
AE.AB + AF.AC = 2AH² (3)
Xét tứ giác AEHF có:
∠HFA = ∠FAE = ∠AEH = 90⁰ (gt)
⇒ AEHF là hình chữ nhật
⇒ AH = EF (4)
Từ (3) và (4) suy ra:
AE.AB + AF.AC = 2EF²
Bài 1
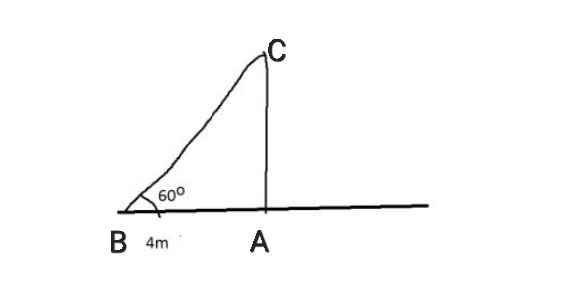 Ta có:
Ta có:
tan B = AC/AB
⇒ AC = AB . tan B
= 4 . tan60⁰
= 4√3 (m)
≈ 7 (m)

Gọi chân cột đèn là điểm A, đỉnh cột đèn là điểm B và bóng của đỉnh cột trên mặt đất là C
Ta có tam giác ABC vuông tại A với \(AC=7,5\left(m\right)\) và \(\widehat{BCA}=42^0\)
Trong tam giác vuông ABC:
\(AB=AC.tan\widehat{BAC}=7,5.tan42^0\approx6,8\left(m\right)\)

Ta có: tan C = A B A C = 6 3 , 5 = 12 7 ⇒ C ^ ≃ 59 0 45 '
Đáp án cần chọn là: C
Bài 3:
Góc tạo bởi tia sáng với mặt đất là $\alpha$
Ta có:
$\tan \alpha=\frac{7}{4}\Rightarrow \alpha=60,26^0$
Bài 4: Không đủ dữ kiện để giải. Bạn xem lại đề.