Tính tổng :S=1+2+2 mũ 2+2 mũ3+....+2 mũ 2015/ 1-2 mũ2016
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đặt tử là T ta có:
2T=2(1+2+22+23+...+22015)
2T=2+22+23+...+22016
2T-T=(2+22+23+...+22016)-(1+2+22+23+...+22015)
T=22016-1
thay T vào tử của S ta được:\(S=\frac{2^{2016}-1}{1-2^{2016}}=-1\)

Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)
Khi n=1 thì ta sẽ có 1^3=1^2(đúng)
Giả sử (1) đúng khi n=k
Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2
Ta sẽ cần chứng minh (1) đúng khi n=k+1
1^3+2^3+...+n^3
=1^3+2^3+...+k^3+(k+1)^3
=(1+2+3+...+k)^2+(k+1)^3
Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)
=(k+1)^2+2*(k+1)*k*(k+1)/2
=(k+1)^2*(1+k)=(k+1)^3
=>1^3+2^3+...+(k+1)^3
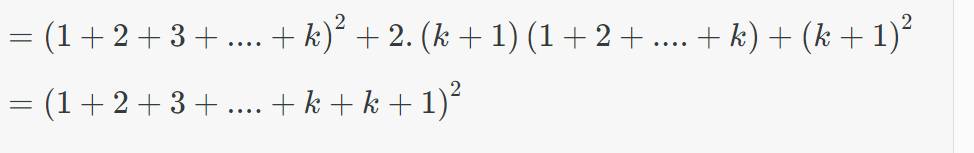
=>ĐPCM

a) \(\left(3^4.57-9^2.21\right):3^5\)
\(=\left(3^4.57-3^4.21\right):3^5\)
\(=\left[3^4\left(57-21\right)\right]:3^5\)
\(=3^4.36:3^5\)
\(=3^4.2^2.3^2:3^5\)
\(=3.4\)
\(=12\)
b) Ta có; \(1^3+2^3+...+9^3=2025\)
\(\Leftrightarrow2^3.\left(1^3+2^3+....+9^3\right)=2^3.2025\)
\(\Leftrightarrow2^3+4^5+...+18^3=16200\)

A = 1+2+22+...+210
=> 2A = 2+22+23+...+211
=> 2A - A = (2+22+23+...+211) - (1+2+22+...+210)
=> A = 211 - 1
B = 1+3+32+...+310
=> 3B = 3+32+33+...+311
=> 3B - B = (3+32+33+...+311) - (1+3+32+...+310)
=> 2B = 311 - 1
=> B = \(\frac{3^{11}-1}{2}\)
A = 1 + 2 1 + 2 2 + 2 3 + ... + 2 9 + 2 10
2A = 2 + 2 2 + 2 3 + 2 4 + ... + 2 10 + 2 11
2A - A = ( 2 + 2 2 + 2 3 + 2 4 + ... + 2 10 + 2 11 )
- ( 1 + 2 1 + 2 2 + 2 3 + ... + 2 9 + 2 10 )
A = 2 11 - 1
A = 2047
B = 1 + 3 1 + 3 2 + 3 3 + ... + 3 9 + 3 10
3B = 3 1 + 3 2 + 3 3 + 3 4 + ... + 3 10 + 3 11
3B - B= ( 3 1 + 3 2 + 3 3 + 3 4 + ... + 3 10 + 3 11 )
- ( 1 + 3 1 + 3 2 + 3 3 + ... + 3 9 + 3 10 )
2B = 3 11 - 1
B = \(\frac{3^{11}-1}{2}\)
B = 88573

Chắc đề thế này!
\(S=1+2+2^2+2^3+2^4+...+2^{2014}\)
\(2S=2+2^2+2^3+2^4+...+2^{2015}\)
\(2S-S=\left(2+2^2+2^3+...+2^{2015}\right)-\left(1+2+2^2+...+2^{2014}\right)\)
\(\Rightarrow2S-S=S=2^{2015}-1< 2^{2015}\Rightarrow S< D\)

\(\Rightarrow2S=2+2^2+2^3+...+2^{101}\)
\(\Rightarrow2S-S=2+2^2+2^3+...+2^{101}-1-2-2^2-...-2^{100}\)
\(\Rightarrow S=2^{101}-1\)

\(S=1+2^1+...+2^{100}\)
\(\Rightarrow2S=2+2^2+...+2^{101}\)
\(\Rightarrow2S-S=2+2^2+...+2^{101}-1-2^1-...-2^{100}\)
\(\Rightarrow S=2^{101}-1\)
Ta có S=\(\frac{1+2+2^2+...+2^{2015}}{1-2^{2016}}\)
Đặt M là tử của 2 ta có
M=1+2+2^2+...+2^2015
2M=2*(1+2+2^2+...+2^2015)
2M=2+2^2+2^3+...+2^2016
2M-M=(2+2^2+2^3+...+2^2016)-(1+2+2^2+...+2^2015)
M=2^2016-1
S=\(\frac{2^{2016}-1}{1-2^{2016}}\)
Ta thấy tử và mẫu của S là 2 số đối nhau.Mà 2 số đối nhau luôn có thương là -1
Nên S=-1