Các điểm A'(-4; 1), B'(2;4), C(2, -2) lần lượt là trung điểm của các cạnh BC, CA và AB của tam giác ABC. Tìm tọa độ đỉnh của tam giác ABC và A’B’C’ trùng nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
8 tháng 11 2017
A B C D
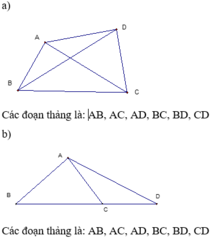
a/ Có 4 đường thẳng, gồm: AB, AC, AD và BD=BC=CD
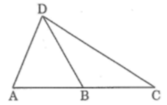
b/ Có tất cả 3 tam giác gồm: ABC, ABD, ACD
QL
4
CM
5 tháng 6 2017
Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số f ( x ) = - 1 4 x ta được:
+) Với M (0; 4), thay x = 0; y = 4 ta được 4 = - 1 4 .0 ⇔ 4 = 0 (vô lý) nên M ∉ (C)
+) Với O (0; 0), thay x = 0 ; y = 0 ta được 0 = - 1 4 .0 ⇔ 0 = 0 (luôn đúng) nên O ∈ (C)
+) Với P (4; −1), thay x = 4 ; y = − 1 ta được −1 = - 1 4 . 4 ⇔ 1 = −1 (luôn đúng) nên P ∈ (C)
+) Với Q (−4; 1), thay x = − 4 ; y = 1 ta được 1 = - 1 4 .(−4) ⇔ 1 = 1 (luôn đúng) nên Q ∈ (C)
+) Với A (8; −2), thay x = 8 ; y = − 2 ta được −2 = - 1 4 .8 ⇔ −2 = −2 (luôn đúng) nên A ∈
Đáp án cần chọn là: A
1 tháng 2 2023
Câu 1: \(9^6\cdot7-3^{12}\cdot4\)
\(=3^{2^6}\cdot7-3^{12}\cdot4\)
\(=3^{12}\cdot7-3^{12}\cdot4\)
\(=3^{12}\left(7-4\right)\)
\(=3^{12}\cdot3\)
\(=3^{13}\)
Câu 2:
a) Số đường thẳng đi qua 2 điểm là: \(3+2+1=6\left(đường\right)\)
b) Các đường thẳng đó là: \(AB;AC;AD;BC;BD;CD\)
A’ là trung điểm của cạnh BC nên -4 =
(xB+ xC)
=> xB+ xC = -8 (1)
Tương tự ta có xA+ xC = 4 (2)
xB+ xC = 4 (3)
=> xA+ xB+ xC =0 (4)
Kết hợp (4) và (1) ta có: xA= 8
(4) và (2) ta có: xB= -4
(4) và (3) ta có: xC = -4
Tương tự ta tính được: yA = 1; yB = -5; yC = 7.
Vậy A(8;1), B(-4;-5), C(-4; 7).
Gọi G la trọng tâm tam giác ABC thì
xG=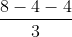
= 0; yG = 
= 1 => G(0,1).
xG’=
; yG’ = 
= 1 => G'(0;1)
Rõ ràng G và G’ trùng nhau.