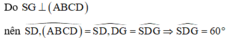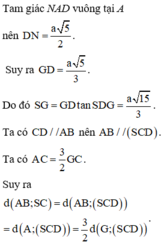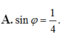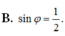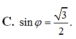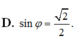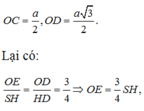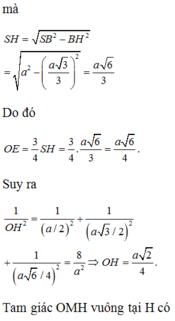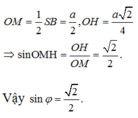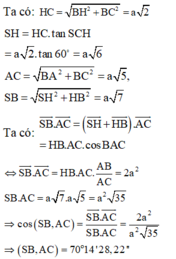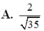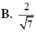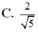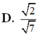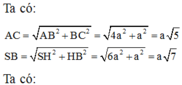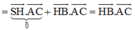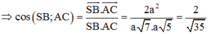Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có \(AB=a,BC=2a\sqrt{a}\). Hình chiếu của S lên mặt phẳng đáy là trọng tâm của tam giác ABC. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 60 độ. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách từ điểm A đến mặt phẳng (SBC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 3 2019
Chọn đáp án A
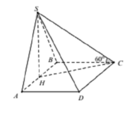
Từ kẻ đường thẳng vuông góc với SC cắt SC tại K.
CM
6 tháng 9 2019
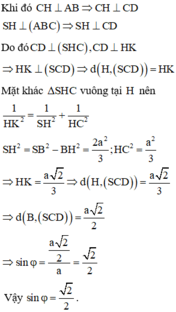
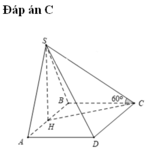
Đáp án C
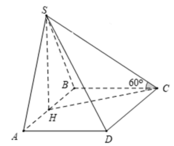
Ta có: H C = B H 2 + B C 2 = a 2
S H = H C . tan S C H = a 2 . tan 60 ∘ = a 6 A C = B A 2 + B C 2 = a 5 , S B = S H 2 + H B 2 = a 7
Ta có: S B → . A C → = S H → + H B → . A C → = H B . A C . cos B A C
⇔ S B → . A C → = H B . A C . A B A C = 2 a 2 S B . A C = a 7 . a 5 = a 2 35 ⇒ c os S B , A C = S B → . A C → S B . A C = 2 a 2 a 2 35 ⇒ S B , A C = 70 o 14 ' 28 , 22 ' '
CM
29 tháng 5 2018
Chọn D.
Phương pháp:
- Gọi M là trung điểm của SD, nhận xét góc giữa SB và (SCD) cũng bằng góc giữa OM và (SCD).
- Xác định góc φ và tính sin φ
Cách giải:
CM
2 tháng 6 2017
Đáp án A
Phương pháp: Sử dụng công thức 
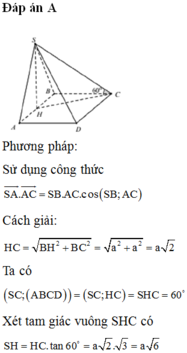
Cách giải: 
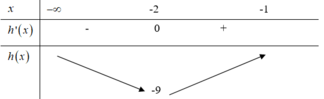
Ta có 
Xét tam giác vuông SHC có 
Ta có:
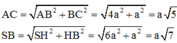
Ta có:
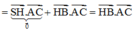
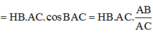
Lại có 
CM
9 tháng 5 2018
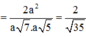
Chọn đáp án A.
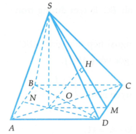
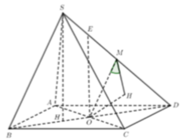
Gọi O là tâm của hình vuông và N là trung điểm của AB.
Khi đó G là giao điểm của AC và DN. Tam giác SGD vuông tại G nên S D G ^ nhọn
