Cho tứ diện đều ABCD có các cạnh bằng a. Gọi M là trung điểm cạnh AB. Xác định vị trí của điểm N trên đường thẳng AC sao cho \(DN\perp CM\). Khi đó, tính khoảng cách giữa hai đường thẳng CM và DN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


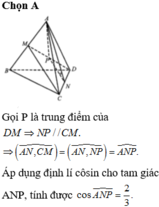
Vẽ \(NP\perp AM\) tại P
\(\hept{\begin{cases}\text{có }AB=a\Rightarrow AM=\sqrt{AB^2+BN^2}=\frac{\sqrt{5}}{2}a\\\text{từ }CM:AM=AD=a\end{cases}}\Rightarrow MP=\frac{-2+\sqrt{5}}{2}a\)
Đặt ND = NP, ta có:
\(x^2+MP^2=MC^2+CN^2\)
\(x^2+\left(\frac{-2+\sqrt{5}}{2}\right)^2a^2=\frac{a^2}{4}+\left(a-x\right)^2\)
\(\Leftrightarrow x^2+\frac{9-4\sqrt{5}}{4}a^2=\frac{a^2}{4}+a^2-2ax+x^2\)
\(\Leftrightarrow a^2\left(\frac{9-4\sqrt{5}}{4}-\frac{1}{4}-1\right)=-2ax\)
\(\Leftrightarrow\left(1-\sqrt{5}\right)a^2=-2ax\)
\(\Leftrightarrow x=\frac{\sqrt{5}-1}{2}a\Rightarrow CN=\frac{3-\sqrt{5}}{2}a\)
\(\Rightarrow MN=\sqrt{CN^2+MC^2}\)
\(MN=\sqrt{\frac{15-6\sqrt{5}}{4}a^2}\)
\(MN=\sqrt{\frac{15-6\sqrt{5}}{2}}a\)
P/s: Ko chắc

a)Độ dài cạnh AN là: 9 * 2/3 = 6 (cm)
Diện tích hình thang ANCD là: (6+9)*9/2 = 67,5 (cm2)

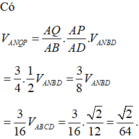

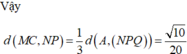
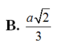
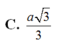
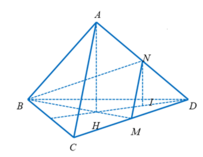

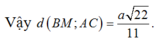
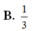
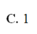

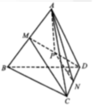
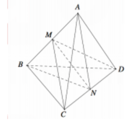
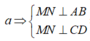
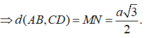
Đặt \(\overrightarrow{DA}=\)\(\overrightarrow{a}\) , \(\overrightarrow{DB}=\overrightarrow{b},\overrightarrow{DC}=\overrightarrow{c}\) với \(\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=\left|\overrightarrow{c}\right|=a\) và \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=\frac{a^2}{2}\) như hình vẽ
Do M là trung điểm AB nên \(\overrightarrow{DM}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}\)
do đó \(\overrightarrow{CM}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}-\overrightarrow{c}\)
Xét điểm \(N\in AC\), giả sử \(\overrightarrow{NA}=t.\overrightarrow{NC}\), \(t\ne1\). Khi đó \(\overrightarrow{DN}=\frac{\overrightarrow{a}-t\overrightarrow{c}}{1-t}\)
Vậy \(DN\perp CM\Rightarrow\overrightarrow{DN}.\overrightarrow{CM}=0\Leftrightarrow\left(\overrightarrow{a}+\overrightarrow{b}-2\overrightarrow{c}\right)\left(\overrightarrow{a}-t\overrightarrow{c}\right)=0\Leftrightarrow t=\frac{1}{2}\)
Từ đó , với \(N\in AC\) mà \(\overrightarrow{NC}=-2\overrightarrow{NA}\) thì \(DN\perp CM\) và khi đó
\(\overrightarrow{DN}=\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{c}\)
Giả sử UV là đoạn vuông góc chung của CM, DN với \(U\in CM,V\in DN\) và \(\overrightarrow{CU}=u\overrightarrow{CM}=\frac{u}{2}.\overrightarrow{a}+\frac{u}{2}.\overrightarrow{b}-u.\overrightarrow{c},\overrightarrow{DV}=v.\overrightarrow{DN}=\frac{2v}{3}.\overrightarrow{a}+\frac{v}{3}.\overrightarrow{c}\)
Từ đó suy ra
\(\overrightarrow{UV}=\overrightarrow{DV}-\left(\overrightarrow{DC}+\overrightarrow{CU}\right)\)
\(=\left(\frac{2v}{3}-\frac{u}{2}\right)\overrightarrow{a}-\frac{u}{2}\overrightarrow{b}+\left(\frac{v}{3}+u-1\right)\overrightarrow{c}\)
Điều kiện \(\overrightarrow{UV}.\overrightarrow{CM}=0\) tương đương với :
\(\frac{1}{2}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{4}-\left(\frac{v}{3}+u-1\right)+\frac{1}{4}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{1}{2}\left(\frac{2v}{3}-\frac{u}{2}\right)+\frac{u}{4}+\frac{1}{4}\left(\frac{v}{3}+u-1\right)+\frac{1}{4}\left(\frac{v}{3}+u-1\right)=0\)
Từ đó ta thu được \(u=\frac{2}{3}\)
Điều kiện \(\overrightarrow{UV}.\overrightarrow{DN}=0\) tương đương với :
\(\frac{2}{3}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{6}+\frac{1}{3}\left(\frac{v}{3}+u-1\right)+\frac{1}{6}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{12}+\frac{1}{3}\left(\frac{v}{3}+u-1\right)=0\)
Từ đó ta thu được \(v=\frac{6}{7}\)
Khi đó, \(\overrightarrow{UV}=\frac{5}{21}\overrightarrow{a}-\frac{7}{21}\overrightarrow{b}-\frac{1}{21}\overrightarrow{c}=\frac{1}{21}\left(5\overrightarrow{a}-7\overrightarrow{b}-\overrightarrow{c}\right)\)
Suy ra \(d\left(CM,DN\right)=UV=\sqrt{\left|\overrightarrow{UV}\right|^2}=\frac{a\sqrt{42}}{21}\)