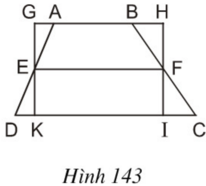
Chứng minh để ra 3 công thức này:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



HƯỚNG DẪN
a) Vai trò của ngành công nghiệp lương thực, thực phẩm
- Thông qua hoạt động chế biến, các sản phẩm nông nghiệp - thuỷ sản vừa có chất lượng cao, lại vừa dễ bảo quản, thuận tiện cho việc chuyên chở.
- Xây dựng ngành công nghiệp này đòi hỏi vốn đầu tư ít hơn nhiều so với các ngành công nghiệp nặng, vốn quay vòng lại nhanh hơn. Việc thu hồi vốn diễn ra sau một thời gian ngắn làm tăng tốc độ tích luỹ cho nền kinh tế.
- Tạo nên một số mặt hàng xuất khẩu chủ lực của nước ta.
- Thúc đẩy việc sản xuất hàng hoá trong nông nghiệp, góp phần làm chuyển dịch cơ cấu kinh tế - xã hội ở nông thôn.
b) Chứng minh nước ta có nhiều thế mạnh để phát triển ngành công nghiệp chế biến lương thực, thực phẩm.
- Nguồn nguyên liệu tại chỗ từ nông nghiệp và thuỷ sản tương đối phong phú. Nhiều vùng chuyên canh quy mô lớn về cây trồng (lúa gạo, cây công nghiệp, cây ăn quả) và vật nuôi (gia súc lớn, gia súc nhỏ, gia cầm, thuỷ sản) đã được hình thành, tạo cơ sở thuận lợi, đảm bảo nguồn nguyên liệu tại chỗ thường xuyên, ổn định cho công nghiệp chế biến.
- Thị trường tiêu thụ rộng lớn, cả trong nước và ngoài nước.
- Cơ sở vật chất kĩ thuật ngày càng được đầu tư phát triển.
- Nguồn lao động dồi dào.
- Chính sách phát triển (công nghiệp chế biến lương thực, thực phẩm là ngành công nghiệp trọng điểm của nước ta).

Chứng minh:4 = 5
-->Ta có
-20 = -20
<=> 25 - 45 = 16 - 36
=> 5^2 - 2.5.9/ 2 = 4^2 - 2.4.9/2
Cộg cả 2 vế với (9/2)^2 để xuất hiện hằg đẳg thức :
5^2 - 2.5.9/2 + (9/2)^2 = 4^2 - 2.4.9/2 + (9/2)^2
<=> (5 - 9/2)^2 = (4 - 9/2 )^2
=> 5 - 9/2 = 4 - 9/2
=> 5 = 4
Các bạn thấy thế nào
Ai đi ngang qua nhớ nha
Chứng minh:4 = 5
-->Ta có
-20 = -20
<=> 25 - 45 = 16 - 36
=> 5^2 - 2.5.9/ 2 = 4^2 - 2.4.9/2
Cộg cả 2 vế với (9/2)^2 để xuất hiện hằg đẳg thức :
5^2 - 2.5.9/2 + (9/2)^2 = 4^2 - 2.4.9/2 + (9/2)^2
<=> (5 - 9/2)^2 = (4 - 9/2 )^2
=> 5 - 9/2 = 4 - 9/2
=> 5 = 4

2x2-2x+2=2(x2-x+1)
\(=2\left(x^2-\frac{1}{2}x-\frac{1}{2}x+\frac{1}{4}+\frac{3}{4}\right)\)
\(=2\left[x\left(x-\frac{1}{2}\right)-\frac{1}{2}\left(x-\frac{1}{2}\right)+\frac{3}{4}\right]=2\left(x-\frac{1}{2}\right)\left(x-\frac{1}{2}\right)+\frac{3}{4}\)
\(=2\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)
Vì \(2\left(x-\frac{1}{2}\right)^2\ge0\Rightarrow2\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\)
=>đa thức vô nghiệm

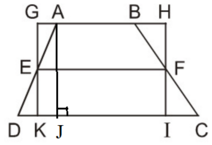
Ta có hình thang ABCD (AB // CD) với đường trung bình EF và hình chữ nhật GHIK như hình vẽ.
Dễ dàng chứng minh:
ΔAEG = ΔDEK, ΔBFH = ΔCFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên SABCD = SGHIK
Mà SGHIK = GH.GK= EF. AJ ( vì GH = EF, GK = AJ)
Nên SABCD = EF. AJ
Lại có:
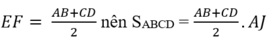
Vậy ta gặp lại công thức tính diện tích hình thang đã học nhưng bằng một phương pháp chứng minh khác.
Mặt khác, ta phát hiện công thức mới: Diện tích hình thang bằng tích của đường trung bình hình thang với đường cao.


Vì kiềm là một loại bazơ tan được trong nước nên tất cả các chất kiềm đều là baz ơ.
Thí dụ: NaOH, KOH, Ba(OH)2.
b) Vì không phảo mọi bazơ đều tan trong nước nên không phải tất cả các bazơ đều là chất kiềm.
Thí dụ: Các bazơ Cu(OH)2,Mg(OH)2, Fe(OH)3 ..không phải là chất kiềm.

– Đoạn mở đầu, tác giả kể một hồi ức thủa học trò: giáo viên đã giao một bài tập để học sinh tự do thể hiện sự khác biệt.
– Đoạn tiếp câu chuyện xoay quanh sự lựa chọn của số động học sinh trong lớp và của riêng J. Lời bàn luận chỉ xuất hiện sau những đoạn kể như vậy.
=> Ở văn bản này, tác giả đi từ thực tế để rút ra điều cần bàn luận. Nhờ cách triển khai này, văn bản không mang tính chất bình giá nặng nề. Câu chuyện làm cho vấn đề bàn luận trở nên gần gũi, nhẹ nhàng.