Cho tam giác ABC. Ở phía ngoài tam giác vẽ các tam giác vuông cân ABD và ACE.
a) C/M : CD = BE và CD\(\perp\)BE ( câu này mik làm được rồi )
b) Kẻ đ/t qua A và vuông góc với BC. C/M : AH đi qua trung điểm của DE
c) Lấy K năm trong tam giác ABD sao cho ABK = 300, BA = BK. C/M : AK = KD.


a) Kẻ DM, EN vuông góc BC.
Xét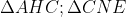 :
:
_ AC = CE
_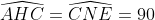
_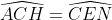 (góc có cạnh tương ứng vuông góc)
(góc có cạnh tương ứng vuông góc)
Nên chúng bằng nhau, suy ra: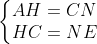
Tương tự: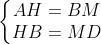
Do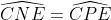 (P là giao của CK và BE, quên vẽ) nên CNEP là tứ giác ntiếp
(P là giao của CK và BE, quên vẽ) nên CNEP là tứ giác ntiếp 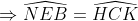
Do đó 2 tam giác vuông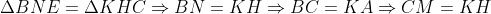
Từ đó: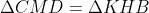
2 tg này có 2 cặp cạnh tg ứng vuông góc là MD, BH và MC, KH nên cặp còn lại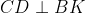
b) Từ a ta có KH, BE, CD là 3 đường cao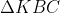 , nên chúng đòng quy tại I.
, nên chúng đòng quy tại I.