Cho 4 đường thẳng phân biệt và gọi S là tập hợp tất cả các giao điểm của các đường thẳng ấy. Số phần tử nhiều nhất nhất có thể của S là...
Ghi lời giải giùm em nha mấy anh chụy...Kíu em zới!!!!!!!!!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BH
3
Những câu hỏi liên quan
BT
14 tháng 3 2017
3 đường thẳng phân biệt ta có 3 giao điểm. Đường thẳng thứ 4 cắt 3 đường thẳng kia nhiều nhất tại 3 điểm nữa.
Vậy nhiều nhất có 6 điểm
2 tháng 2 2017
bài 2 nè:
Ta có: \(\frac{10+x}{17+x}\)= \(\frac{3}{4}\)
==> (10+x)x4 = (17+x)x3
=> 40+ 4x = 51 + 3x
=> 51 - 40 = 4x - 3x
=> x = 11
nếu bạn cho tiền thì ib mềnh nha :)
CM
13 tháng 4 2019
Phương trình hoành độ giao điểm: - x 2 + 2 x + 3 = m x ⇔ x 2 + m - 2 x - 3 = 0 1
Dễ thấy (1) luôn có 2 nghiệm phân biệt vì a c = 1 . - 3 = - 3 < 0
Khi đó (d) cắt (P) tại hai điểm phân biệt A x 1 ; m x 1 , B x 2 ; m x 2 , với x 1 , x 2 là nghiệm phương trình (1). Theo Viét, có: x 1 + x 2 = 2 - m , x 1 x 2 = - 3 x 1 x 2 = - 3
I là trung điểm
A B ⇒ I = x 1 + x 2 2 ; m x 1 + m x 2 2 = 2 − m 2 ; − m 2 + 2 m 2
Mà I ∈ ( Δ ) : y = x − 3 ⇒ − m 2 + 2 m 2 = 2 − m 2 − 3 ⇔ m 2 − 3 m − 4 = 0
⇔ m = − 1 = m 1 m = 4 = m 2 ⇒ m 1 + m 2 = 3
Đáp án cần chọn là: D
CM
20 tháng 11 2017
Mặt cầu (S) có tâm I (1;0;-2) và bán kính R=2.
Đường thẳng d đi qua điểm N (2; 0; m-1) và có véc tơ chỉ phương 
Điều kiện để d cắt (S) tại hai điểm phân biệt là d (I; (d))<R
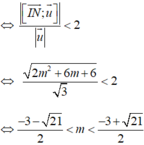
Khi đó, tiếp diện của (S) tại A và B vuông góc với IA và IB nên góc giữa chúng là góc (IA;IB).
Vậy T= {-3;0}. Tổng các phần tử của tập hợp T bằng -3.
29 tháng 7 2023
Tọa độ A là:
x=0 và y=0(2m+1)+m-2=m-2
=>OA=|m-2|
Tọa độ B là:
y=0 và (2m+1)x+m-2=0
=>x=(2-m)/(2m+1) và y=0
=>OB=|(m-2)/(2m+1)|
Để ΔOAB cân thì OA=OB
=>|m-2|=|m-2|/|2m+1|
=>|m-2|(1-1/|2m+1|)=0
=>m-2=0 hoặc 2m+1=-1 hoặc 2m+1=1
=>S={2;-1;0}
Tổng các phần tử của S là 1
2 đường thẳng thì cắt nhau tại 1 điểm
n đường thẳng sẽ cắt nhau tại \(C^{n_{ }}_2\) điểm ( tổ hợp nhé)
vậy 4 đường sẽ có \(C^4_2\)= 6 điểm
thanks, nhưng e ko hiểu, mới lớp 6 mà