- Tìm n
- 4n - 5 chia hết cho 2n - 1
- 12 - n chia hết cho 8 - n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NH
4
Những câu hỏi liên quan
24 tháng 9 2021
\(a,\Rightarrow n+3\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Rightarrow n\in\left\{-8;-4;-2;2\right\}\\ b,\Rightarrow n+3+5⋮n+3\\ \Rightarrow5⋮n+3\\ \Rightarrow n+3\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Rightarrow n\in\left\{-8;-4;-2;2\right\}\\ c,\Rightarrow2\left(2n-1\right)-3⋮2n-1\\ \Rightarrow3⋮2n-1\\ \Rightarrow2n-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Rightarrow n\in\left\{-1;0;1;2\right\}\\ d,\Rightarrow8-n+4⋮8-n\\ \Rightarrow4⋮8-n\\ \Rightarrow8-n\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Rightarrow n\in\left\{12;10;9;7;6;4\right\}\)
23 tháng 11 2017
dài qá, lm 1 câu thôi, chỗ cn lại tương tự
Ta có :
\(n+8⋮n+3\)
Mà \(n+3⋮n+3\)
\(\Leftrightarrow5⋮n+3\)
\(\Leftrightarrow n+3\inƯ\left(5\right)\)
\(\Leftrightarrow\orbr{\begin{cases}n+3=1\\n+3=5\end{cases}}\) \(\Leftrightarrow\orbr{\begin{cases}n=-2\\n=2\end{cases}}\)
Vậy ..
DK
2
23 tháng 11 2017
a) Ta có \(\frac{12-n}{8-n}=\frac{8-n+4}{8-n}=1+\frac{4}{8-n}\)
\(12-n⋮8-n\Leftrightarrow4⋮8-n\)
hay \(8-n\inƯ\left(4\right)=\left\{1;-1;2;-2;4;-4\right\}\)
\(\Rightarrow n\in\left\{7;9;6;10;4;12\right\}\)
b) Ta có \(\frac{4n+5}{2n+1}=\frac{4n+2+3}{2n+1}=2+\frac{3}{2n+1}\)
\(4n+5⋮2n+1\Leftrightarrow3⋮2n+1\)
23 tháng 11 2017
\(\Rightarrow2n+1\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
\(\Rightarrow n\in\left\{0;-1;1;-2\right\}\)
Mình lỡ bấm gửi trước khi làm xong, bài tiếp theo nè.
1 tháng 11 2015
n + 8 chia hết cho n + 3
=> n + 3 + 5 chia hết cho n + 3
=> n + 3 thuộc Ư ( 5 )
=> n + 3 = { 1 , - 1 , 5 , -5 )
=> n = { -2 , - 4 , 2 , -8 }
mấy câu kia tương tự
28 tháng 10 2019
\(n-5⋮n-3\)
\(n-3+2⋮n-3\)
Vì \(n-3⋮n-3\)
\(2⋮n-3\)
\(\Rightarrow n-3\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Ta có bảng
| n-3 | -1 | 1 | -2 | 2 |
| n | 2 | 4 | 1 | 5 |
tự lm tiếp phần sau ... hc tốt
LT
4
3 tháng 9 2015
4n - 5 chia hết cho 2n + 1
=> 4n + 2 - 7 chia hết cho 2n + 1
Mà 4n + 2 chia hết cho 2n + 1
=> -7 chia hết cho 2n + 1
3 tháng 9 2015
a)4n-5 chia hết cho 2n+1
=>4n+2-7 chia hết cho 2n-1
=>-7 chia hết cho 2n-1
=> 2n+1 thuộc vào tập hợp Ư(7)=(1;-1;7;-7)
ta có bảng sau
| 2n+1 | 1 | -1 | 2 | -2 |
| n | 0 | -19 loại | 1/2(loại) | 3/2(loại) |
vậy..................................................................................................................
b) 12- n chia hết cho 8-n
=>4+8- n chia hết cho 8-n
=>8-n thuộc Ư(4)=(1;-1;2;-2;4;-4)
ta có bảng sau:
| 8-n | 1 | -1 | 2 | -2 | 4 | -4 |
| n | 7 | 9 | 6 | 10 | 4 | 12 |
vậy.....................................................................................................................
GK
3
BT
15 tháng 1 2018
a/ Ta có: 2n-7=2n+6-13=2(n+3)-13
Nhận thấy, 2(n+3) chia hết cho n+3 với mọi n
=> Để 2n-7 chia hết cho n+3 => 13 chia hết cho n+3
=> n+3=(-13,-1,1,13)
| n+3 | -13 | -1 | 1 | 13 |
| n | -16 | -4 | -2 | 10 |
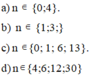
a. 4n - 5 chia hết cho 2n - 1
=> 2(2n - 1) - 3 chia hết cho 2n - 1
=> 3 chia hết cho 2n - 1( vì 2(2n - 1) chia hết cho 2n - 1)
=> \(2n-1\inƯ\left(3\right)\)mà Ư(3) = { +-1 ; +-3}
Ta có bảng sau:
- Phép chia a cho c (c ≠ 0) được thương là q và số dư là r thì:
a = c . q + r (với 0 ≤ r < c; nếu r = 0 thì a chia hết cho c)
- Nếu a và b đều chia hết cho c thì tổng (a + b) và hiệu (a - b) của chúng cũng chia hết cho c. (Chú ý: nếu cả a và b đều KHÔNG chia hết cho c thì không thể suy ra tổng/hiệu của chúng cũng KHÔNG chia hết cho c, ví dụ 3 và 1 đều không chia hết cho 4 nhưng tổng 3 + 1 lại chia hết cho 4).
- Nếu a = b + d, mà biết b chia hết cho q thì suy ra a chia hết cho q khi và chỉ khi d cũng chia hết cho q.
- Dấu hiệu chia hết 2,5, 10: Dựa trên chữ số cuối cùng, một số có chữ số tận cùng là C thì có thể biểu diễn dạng (xem phần Cấu tạo số):
aC = a0 + C = a.10 + C
Vì a.10 chia hết cho 2, 5, 10 nên một số chia hết cho 2, 5, 10 khi và chỉ khi chữ số tận cùng C chia hết cho 2, 5, 10
- Dấu hiệu chi hết cho 3 và 9: Một số cấu tạo bởi các chữ số A, B, C, D có thể biểu diễn dưới dạng (xem phần Cấu tạo số):
ABCD = 1000.A + 100.B + 10.C + D
= (999.A + A) + (99.B + B) + (9.C + C) + D
= 999.A + 99. B + 9.C + (A + B + C + D)
Mà các số 999.A, 99.B, 9.C đều chia hết cho 3 và 9 nên số ABCD chia hết cho 3 hoặc 9 nếu tổng các chữ số của nó A + B + C + D chia hết cho 3 hoặc 9.
- Số chia hết cho 4 thì chia hết cho 2, số chia hết cho 9 thì chia hết cho 3 (ngược lại không đúng).
II. Các ví dụ
Ví dụ 1:
Tìm hai số tự nhiên biết số lớn gấp 12 lần số bé và thương của hai số đó gấp 2 lần số bé?
Giải:
Vì Số lớn = 12 x số bé
nên Số lớn : số bé = 12
Vậy thương của 2 số đó bằng 12
Khi đó, số bé bằng: 12 : 2 = 6
Và Số lớn bằng: 12 x 6 = 72
-----------------------
Ví dụ 2:
Tìm hai chữ số a và b để số a78b đồng thời chia hết 2, 3, 5, 9?
Giải
Số vừa chia hết cho 2 thì có chữ số tận cùng là 0, 2, 4, 6, hoặc 8.
Số chia hết cho 5 thì có tận cùng là 0 hoặc 5.
Vậy số vừa chia hết cho 2 và vừa chia hết cho 5 thì có chữ số tận cùng phải bằng 0. Suy ra b = 0.
Ta được số a780.
Số chia hết cho 9 thì chia hết cho 3, mà để chia hết cho 9 thì tổng các chữ số chia hết cho 9 hay a + 7 + 8 + 0 = a + 15 chia hết cho 9.
Lần lượt thay a = 0; 1; ..; 9 vào thì thấy chỉ có a = 3 làm cho a + 15 chia hết cho 9.
Đáp số: a = 3, b = 0; Số cần tìm là: 3780
-----------------------
Ví dụ 3:
Tìm số nhỏ nhất khác 0 chia hết cho 2, 3,4, 5, 6, 7?
Giải
Vì một số chia hết cho 4 thì chia hết cho 2 (do 4 chia hết cho 2)
Và số chia hết cho cả 2 và 3 thì chia hết cho 6.
Nên số chia hết cho cả 3 và 4 sẽ chia hết cho cả 2 và 6
Vậy số nhỏ nhất chia hết cho 2,3,4,5,6,7 là: 3 x 4 x 5 x 7 = 420 (ta không nhân với 2 và 6 để được số nhỏ nhất)
Đáp số: 420
-----------------------
Ví dụ 4:
Tìm số tự nhiên nhỏ nhất khác 1 sao cho khi chia cho 2, 3, 4, 5, 7 đều dư 1.
Giải:
Gọi số cần tìm là a.
a chia 2; 3; 4; 5; 7 dư 1 nên a - 1 chia hết cho 2; 3; 4; 5; 7.
Vì số chia hết cho 4 sẽ chia hết cho 2, Suy ra a -1 = 3 x 4 x 5 x 7 = 420
Vậy a = 420 + 1 = 421.
Đáp số: 421.
-----------------------
Ví dụ 5:
Tìm số tự nhiên bé nhất chia cho 2 dư 1, chia cho 3 dư 2,chia cho 4 dư 3, chia cho 5 dư 4.
Giải:
Gọi số cần tìm là a.
a chia cho 2 dư 1, chia cho 3 dư 2, chia cho 4 dư 3, chia cho 5 dư 4 nên a + 1 chia hết cho 2, 3, 4, 5.
Số chia hết cho 4 sẽ chia hết cho 2 nên số chia hết cho đồng thời 2, 3, 4, 5 là 3 x 4 x 5 = 60.
Vậy a + 1 = 60
Suy ra a = 60 - 1 = 59.
Đáp số: 59.
-----------------------
III. Đọc thêm
[1] Các dạng toán chia hết, dấu hiệu chia hết trên Online Math:
+ Lớp 3:
/hoctoan/476/Phép-chia-hết-và-chia-có-dư
+ Lớp 4, 5:
/hoctoan/605/Dấu-hiệu-chia-hết-cho-2-3-5-9-10
/hoctoan/739/Chia-hết-và-chia-có-dư---chia-cho-2-3-5-9-10
/hoctoan/740/Dấu-hiệu-chia-hết-cho-4-8-11
/hoctoan/829/Chia-hết-và-chia-có-dư---nâng-cao
[2] Các bài toán chia hết và chia có dư do các thành viên đưa lên Online Math:
/hoi-dap/tag/dấu-hiệu-chia-hết.html
/hoi-dap/tag/Chia-hết-và-chia-có-dư.html