Tại hai điểm A và B cách nhau 16 cm trên mặt nước dao động cùng tần số 50 Hz, ngược pha, vận tốc truyền sóng trên mặt nước 100 cm/s. Trên đoạn AB số điểm dao động với biên độ cực đại là
A.14.
B.15.
C.16.
D.17.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giữa M và đường trung trực của AB có hai đường cực đại khác tức là M nằm ở đường cực đại thứ k = 3. (Vì đường trung trực của AB với AB cùng pha là cực đại với k = 0)
=> \(AM - BM = 3 \lambda\)
=> \(20 - 15.5 = 3 \lambda \)
=>\(3 \frac{v}{f} = 4,5cm\)
=>\(f = \frac{3v}{4,5} = 20Hz.\)
Chọn đáp án. A

Đáp án C
+ Bước sóng: λ = v/f = 0,6/40 = 1,5cm
+ Số cực đại giao thoa trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thoả mãn:
- A B λ < k < A B λ ⇔ - 10 1 , 5 < k < 10 1 , 5 ⇔ - 6 , 67 < k < 6 , 67 ⇒ k = 0 ; ± 1 , ± 2 , . . . . , ± 6
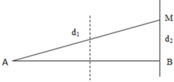
+ Ta có: S A M B = 1 2 A B . M B ⇒ ( S A M B ) m i n ⇔ ( M B ) m i n ⇔ M thuộc cực đại ứng với kmax => d1 – d2 = 6λ = 9cm.
+ Áp dụng định lí Pi – ta – go trong tam giác vuông AMB có:
A B 2 + d 2 2 = d 1 2 ⇔ 10 2 + d 2 2 = ( d 2 + 9 ) 2 ⇒ d 2 = 19 18 c m = M B ⇒ S A M B = 1 2 A B . M B = 1 2 . 10 . 19 18 = 5 , 28 c m 2

Đáp án C

+ Bước sóng: λ = v/f = 0,6/40 = 1,5cm
+ Số cực đại giao thoa trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thoả mãn:

+ Áp dụng định lí Pi – ta – go trong tam giác vuông AMB có:
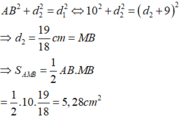

\(\lambda = v/f = 1,5cm.\)
Số gợn lồi (cực đại) thỏa mãn:
\(-AB < d_2-d_1 < AB \Rightarrow -AB < (k+\frac{\triangle\varphi)}{2 \pi}\lambda < AB \\ \Rightarrow -9 < k \lambda < 9 \\ \Rightarrow -6 < k < 6 \\ \Rightarrow k = -5,...,0,1,...5.\)
Có 11 gợn lồi.

Đáp án C
Phương pháp: Δ φ = 2 π d λ
Cách giải:
+ Áp dụng hệ thức lượng trong tam giác vuông OMN có đường cao OH:
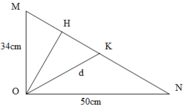
1 O H 2 = 1 O M 2 + 1 O N 2 ⇔ 1 O H 2 = 1 34 2 + 1 50 2 ⇒ O H = 28,1 c m
+ Gọi d là khoảng cách từ O đến K (K là 1 điểm bất kì trên MN)
+ Độ lệch pha giữa K và O là: Δ φ = 2 π d λ
+ Để K dao động cùng pha với O thì: Δ φ = 2 π d λ = 2 k π ⇒ d = k λ
+ Số điểm dao động cùng pha với o trên đoạn MN bằng số giá trị k nguyên thoả mãn:
28,1 ≤ k λ ≤ 34 ⇒ 7,025 ≤ k ≤ 8,5 ⇒ k = 8 28,1 < k λ ≤ 50 ⇒ 7,025 < k ≤ 12,5 ⇒ k = 8 ; 9 ; 10 ; 11 ; 12
Có 6 giá trị của k thoả mãn ⇒ trên đoạn MN có 6 điểm dao động cùng pha với nguồn
\(\lambda = v/f = 100/50 = 2cm.\)
\(\triangle \varphi = \pi\)
Số điểm dao động cực đại thỏa mãn:
\(-AB < d_2-d_1 < AB \Rightarrow -AB < (k+\frac{\triangle\varphi)}{2 \pi}\lambda < AB \\ \Rightarrow -16 < (k + 1/2)\lambda < 16 \\ \Rightarrow -8,5 < k < 7,5 \\ \Rightarrow k = -8,-7,...,0,1,...7. \)
Có 16 điểm dao động với biên độ cực đại.