Sóng dọc truyền trên 1 sợi dây dại lí tưởng với f=50Hz, vận tốc sóng là 200cm/s, biên độ sóng là 5cm. tìm khoảng cách lớn nhất giữa 2 điểm A,B.
Biết A,B nằm trên sợi dây, khi chưa có sóng lần lượt cách nguồn một khoảng là 20cm và 42cm.
mình gặp ít bài sóng dọc nên khó hình dung. chỉ biết cách giải thế này
giải
lamđa= 4cm
suy ra AB= 42-20=22cm = 5,5 lamđa. suy ra 2 điểm dao động ngược pha
giả sử phương trình dao động tại A là x1=5cos(wt) suy ra tại B là x2=5cos(wt + pi)
khoảng cách AB (khi có sóng là: 42 -20 + (x1-x2) = 22 + 10cos (wt) (*)
suy ra AB max = 32
mình không hiểu ở đoạn (*) sao lại cộng với (x1-x2) bạn vẽ hình giúp mình được không. :d

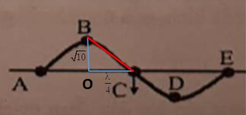
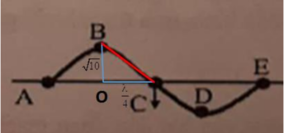



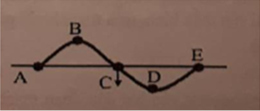
Vì là sóng dọc nên phương dao động trùng phương truyền sóng.
O A B 20 42 u1 u2
Chọn O là gốc tọa độ, trong quá trình dao động tọa độ của A, B lần lượt là:
\(\begin{cases}x_A=20+u_1\\x_B=42+u_2\end{cases}\)
Khoảng cách giữa 2 điểm là: \(\Delta x=x_B-x_A=\left(42+u_2\right)-\left(20+u_1\right)=22+\left(u_2-u_1\right)=22-10\cos\left(\omega t\right)\)
Do đó, khoảng cách max giữa 2 điểm là: 22+ 10 = 32 cm.