Phân tích một mẫu gỗ cổ và một khúc gỗ vừa mới chặt có đồng vị phóng xạ C14 với chu kì bán rã 5600 năm. Đo độ phóng xạ của hai khúc gỗ thì thấy độ phóng xạ của khúc gỗ vừa mới chặt gấp 1,2 lần của khúc gỗ cổ. Khối lượng của mẫu gỗ cổ gấp đôi khối lượng khúc gỗ mới chặt. Tuổi của mẫu gỗ cổ là
A. 4903 năm.
B. 1473 năm.
C. 7073 năm.
D. 4127 năm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

độ phóng xạ \(\beta^-\) của một tượng gỗ bằng 0,8 lần độ phóng xạ của một khúc gỗ cùng khối lượng lúc mới chặt
\(\Rightarrow\) Ht= 0,8Ho AD\(Ht=Ho.2^{-\frac{t}{T}}\)\(\Rightarrow\) t = 1803
Phương pháp: Độ phóng xạ H = H0.2-t/T
Cách giải:
H = 200; H0 = 1600
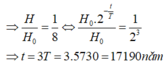
Đáp án D

Đáp án D
Phương pháp: Độ phóng xạ H = H 0 . 2 - t / T
Cách giải:
H = 200; H 0 = 1600
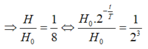
=> t = 3T = 3.5730 = 17190 năm

Tỉ số giữa độ phóng xạ của tượng gỗ (sau thời gian t) so với độ phóng xạ của gỗ lúc mới chặt
\(\frac{H}{H_0}= 0,8= 2^{-\frac{t}{T}}\)
=> \(t = 0,32 T = 1802,8.( năm)\)
Như vậy tượng gỗ có gần 1803 năm tuổi.

Xét tỉ số giữa độ phóng xạ ở thời điểm \(t\) và độ phóng xạ ban đầu ( không cần chuyển đơn vị của độ phóng xạ từ phân rã / phút sang phân rã / giây vì dùng phép chia hai độ phóng xạ cho nhau.)
\(\frac{H}{H_0}= 2^{-\frac{t}{T}}= \frac{1}{8}= 2^{-3}.\)
=> \(t = 3T= 3.5730 = 17190 \)(năm).


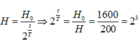
Độ phóng xạ của khúc gỗ mới chặt: \(H_0 = \lambda N_0\)
Độ phóng xạ của khúc gỗ cổ: \(H(t) = H'_{0}. 2^{-t/T} = \lambda. N'_{0} .2^{-t/T}\)
=> \(\frac{H_1}{H_2} = \frac{N_{0}}{N'_{0}} \frac{1}{2 ^ {t/T}} = 1,2.(1)\)
Lại có khối lượng của khúc gỗ cỗ lớn gấp đôi khối lượng của khúc gỗ mới chặt => \(m_0 ' = 2m_0 => \frac{N'_{0}}{N_0} = 2.(2)\)
Thay (2) vào (1) ta được: \(2 ^{t/T} = 2,4 => t = T \log_22,4 \approx 7072,9 \) năm.
Vậy tuổi của mẩu gỗ là: 7073 năm.
Chọn đáp án.C.7073 năm.