Đặt điện áp u = Uocos(ωt) (giá trị không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở R, tụ điện có điện dung C, cuộn cảm thuần có độ tự cảm L thay đổi được. Khi L=L1 và L=L2; điện áp hiệu dụng ở hai đầu cuộn cảm có cùng giá trị; độ lệch pha của điện áp ở hai đầu đoạn mạch so với cường độ dòng điện lần lượt là 0,56 rad và 0,98 rad. Khi L=L0; điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại; hệ số công suất của đoạn mạch lúc này có giá trị xấp xỉ bằng
A. 0,58
B. 0,72
C. 0,83
D. 0,67
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Khi ω < 1 L C ⇔ ω L < 1 ω C ⇔ Z L < Z C không xảy ra cộng hưởng vì thế UR ≠ U ( A sai) và UR < U ( B đúng)
tan φ = Z L - Z C R < 0 => φ = φu – φi < 0 => φu<φi (C và D sai)

Đáp án A
Phương pháp: Ta có: Khi L = L1 thì UAM1 = UR1 = U Khi L = L2 thì
![]()
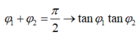
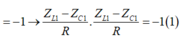
Mặt khác: ta có:
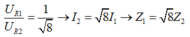
![]()
![]()
Chia cả hai vế của (2) cho (ZL2 - ZC) kết hợp với (1), Ta được:
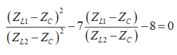
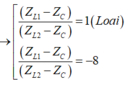
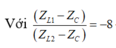
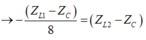
Thay vào (1)
![]()
Hệ số công suất của mạch khi L=L:
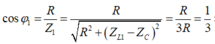
=>Chọn A

Đáp án D
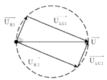
+ Biểu diễn vecto các điện áp.
→ Với trường hợp ![]() ta dễ dàng tìm được:
ta dễ dàng tìm được:
![]()

Chọn A.
Vì khi L hoặc C hoặc f thay đổi để P m a x khi cộng hưởng nên Z L = Z C ⇔ ω 2 L C = 1 .

Khi L = L 1 thì dòng điện cùng pha với điện áp → hiện tượng cộng hưởng → Z C = Z L 1 = 2 π f L 1 .
Khi L = L 2 xảy ra cực đại điện áp hiệu dụng trên cuộn dây Z L 2 = R 2 + Z C 2 Z C ⇔ 2 π f L 2 = 50 2 + 2 π f L 1 2 2 π f L 1 → f = 25 Hz.
Đáp án A

Đáp án A
tan φ = Z L - Z C R ⇒ Z L - Z C = R tan φ ⇒ Z L = R tan φ + Z C
U L = I Z L = U Z L R 2 + ( Z L - Z C ) 2 = U ( R tan φ + Z C ) R 2 + R 2 tan 2 φ = U R ( R sin φ + Z C cos φ )
U L = U R R 2 + Z C 2 cos ( φ - φ 0 ) = U L m a x cos ( φ - φ 0 ) với tan φ 0 = R Z C
Theo bài: U L = 0 , 5 U L m a x ; φ 0 = α ; φ = 0 , 5 α nên cos ( α - 0 , 5 α ) = 0 , 5 ⇒ α = 60 o
tan 60 o = R Z C = 3

Đáp án C
Khi 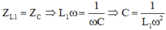
mạch có cộng hưởng ( L 1 = hằng số)
Khi 
![]()
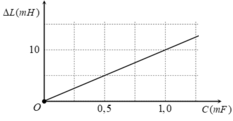
=> Dạng y = a x 2 → Một nhánh của Parabol
Khi
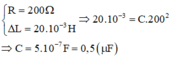

Chọn đáp án C
+ Khi ![]()
![]() mạch có cộng hưởng (L1= hằng số)
mạch có cộng hưởng (L1= hằng số)
+ Khi 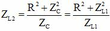
![]()
![]() Dạng
Dạng ![]() → Một nhánh của Parabol
→ Một nhánh của Parabol
+ Khi 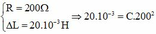
![]()
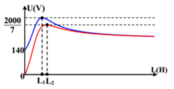

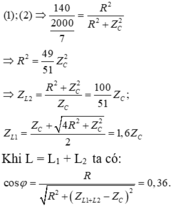
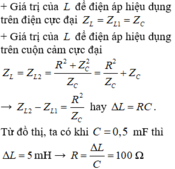
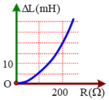
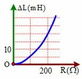
Mình giải thích rõ hơn công thức của bạn Nguyễn Trung Thành
Nhận xét:
+ Khi L thay đổi thì góc b và c không đổi (do R và ZC không đổi).
+ Khi L = L0 để UL max thì a0 + b = 900.
Áp dụng định lí hàm số sin trong tam giác OULUC:
\( \frac{U_L}{\sin(a+b)}=\frac{U}{\sin c}=const\)
\(\Rightarrow\frac{U_L}{\sin(a_1+b)}=\frac{U_L}{\sin(a_2+b)}\Rightarrow \sin(a_1+b)=\sin(a_2+b)\Rightarrow a_1+b=\pi-(a_2+b)\)
\(\Rightarrow a_1+a_2=\pi-2b\) Mà \(a_0+b=\frac{\pi}{2}\Rightarrow 2a_0=\pi-2b\)
\(\Rightarrow a_1+a_2=2a_0\)
Hay: \(\varphi_0=\frac{\varphi_1+\varphi_2}{2}\)
Áp dụng công thức: \(\varphi_0=\frac{\varphi_1+\varphi_2 }{2}\Rightarrow\varphi_0=\frac{0,56+0,98 }{2}=0,77\)
\(\Rightarrow \cos\varphi_0=\cos0,77=0,72\)
Đáp án B.