Mọi người giúp dùm mình bài này với
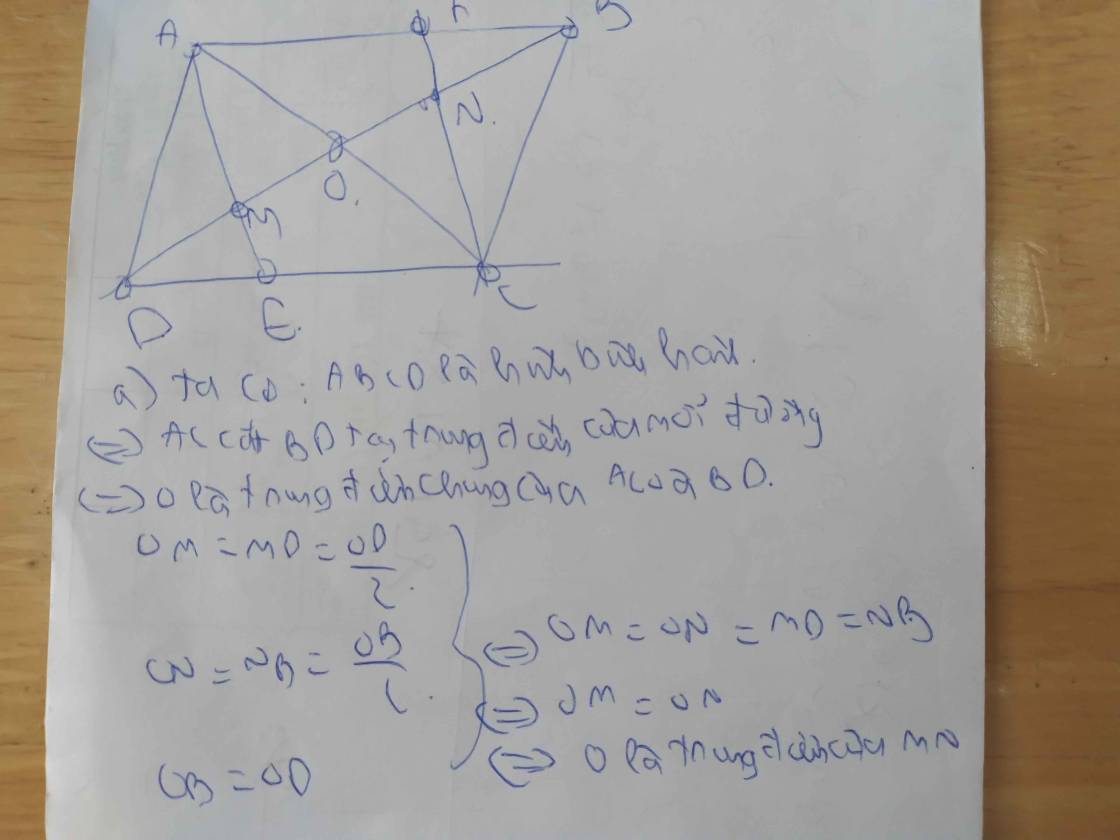
1) cho hình bình hành ABCD với O là giao điểm của hai đường chéo. M và N lần lượt là trung điểm OD và OB .GỌI E là giao điểm của am và cd . F là giao điểm của CN và AB .
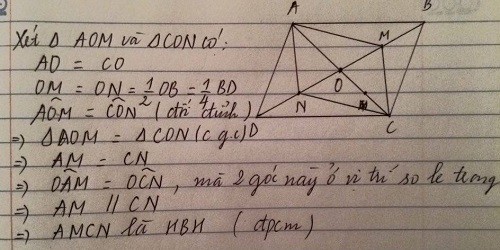
a) cm AMCN là hình bình hành
b) cm AECF là hình bình hành
C) cm e và f đối với nhau qua o
d) cm de=1/2 ec