Sắp xếp các phân số theo thứ tự từ nhỏ đến lớn: − 19 /30 ; − 5/ 9 ; 0 ; − 25/ 47 ; 124/ 2011 ; − 24/ 35 ; − 23 /49 . giúp mik với các bạn giải thích từng bước giải giúp mik nhé!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Dũng
CTVVIP
23 tháng 8 2023
Ta có: \(\dfrac{5}{19}\)< \(\dfrac{7}{19}\)< \(\dfrac{15}{19}\) <\(\dfrac{17}{19}\)
a) Các phân số sắp xếp theo thứ tự từ bé đến lớn: \(\dfrac{5}{19}\); \(\dfrac{7}{19}\); \(\dfrac{15}{19}\); \(\dfrac{17}{19}\)
b) Các phân số sắp xếp theo thứ tự từ lớn đến bé: \(\dfrac{17}{19}\); \(\dfrac{15}{19}\); \(\dfrac{7}{19}\); \(\dfrac{5}{19}\)
PT
2
21 tháng 6 2023
a: -10/8<-1
-19/19=-1
-1<-2/10<0
0<5/12<1<17/15
=>17/15>1>5/12>-2/10>-19/19>-10/8
b: -1/3=-4/12; -5/12=-5/12; -3/4=-9/12; -1/4=-3/12; -7/12=-7/12
=>-3/4<-7/12<-5/12<-1/3<-1/4
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
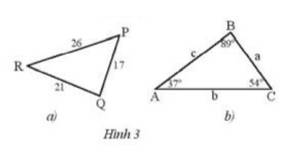
a) Ta có độ dài các cạnh tam giác PQR theo thứ tự từ nhỏ đến lớn là PQ, QR, RP
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ra có các góc tam giác PQR theo thứ tự từ nhỏ đến lớn là R, P, Q
b) Ta có số đo các góc theo tứ tự từ nhỏ đến lớn của tam giác ABC là A, C, B
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ta có các cạnh tam giác ABC theo thứ tự từ nhỏ đến lớn là a, c, b.
15 tháng 2 2018
\(\frac{1}{7};\frac{3}{7};\frac{1}{3}\)từ bé đến lớn đó bn đổi lại giúp mk nha
\(\frac{7}{3};\frac{3}{1};\frac{7}{1}\)từ bé đến lớn đó
15 tháng 2 2018
a) 1/3 ; 1/7 ; 3/7
Thứ tự từ lớn đến bé là : 3/7 ; 1/3 ; 1/7
b)3/1 ; 7/1 ; 7/3
Thứ tự từ bé đến lớn là : 7/3 ; 3/1 ; 7/1
C
24 tháng 4 2022
a)\(\dfrac{8}{15}< \dfrac{11}{15}< \dfrac{15}{15}< \dfrac{16}{15}< \dfrac{17}{15}< \dfrac{19}{15}\)
b)\(\dfrac{19}{42}< \dfrac{19}{35}< \dfrac{19}{21}< \dfrac{19}{19}< \dfrac{19}{17}\)
c)\(\dfrac{8}{10}< \dfrac{6}{7}< \dfrac{27}{25}< \dfrac{16}{14}\)
24 tháng 4 2022
a) 8/15 ; 11/15 ; 15/15 ; 16/15 ; 17/15 ; 19/15
b) 19/42 19/35 ; 19/21 ; 19/19 ; 19/17
c) 8/10 ; 6/7 ; 27/25 ; 16/14
1
K
15 tháng 2 2019
a)\(\frac{3}{7};\frac{1}{3};\frac{1}{7}.\)
b)\(\frac{7}{3};\frac{3}{1};\frac{7}{1}.\)
T**k mik nhé!
1 tháng 8 2017
-124/-2017;0;-24/35;-19/30;-5/9;-25/47;23/-49
tk mk nha, mk đg bị âm điểm
\(\dfrac{-24}{35}< \dfrac{-19}{30}< \dfrac{-5}{9}< \dfrac{-25}{47}< \dfrac{-23}{49}< 0< \dfrac{124}{2011}\)