c/m rằng trong hình thang cân hiệu bình phương của đường chéo và cạnh bên =tích 2 đáy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
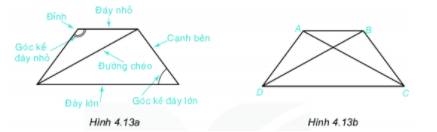
1) Đỉnh: A, B, C, D
Đáy lớn: DC
Đáy nhỏ: AB
Đường chéo: AC, BD
Cạnh bên AD, BC
2) Dùng thước thẳng hoặc compa, ta đo được: AD = BC; AC = BD
Vậy: Hai cạnh bên hình thang cân bằng nhau
Hai đường chéo hình thang cân bằng nhau.
3) Khi đặt eke vuông góc với AB ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
Vậy hai đáy của hình thang cân song song với nhau.
4) Hai góc kề một đáy của hình thang bằng nhau.
+ Bạn vẽ hình như sau: hình thang cân ABCD có đáy nhỏ là AB và đáy lớn là CD
+ Từ C và D hạ lần lượt các đường vuông góc với AB lần lượt cắt AB tại E và F
+ Xét hai tam giác vuông BCE và tam giác vuông ADF có
CE=DF (đường cao của hình thang
BC=AD (hai cạnh bên hình thang cân)
^ADF=^BCE (cùng phụ với ^ADC=BCD)
=> tg BCE=tg ADF (c.g.c) => AF=BE=2AF
+ Xét tam giác vuông BDF có
\(BD^2=DF^2+BF^2=DF^2+\left(AB+AF\right)^2\)
+ Xét tg vuông ADF có
\(AD^2=DF^2+AF^2\)
=> \(BD^2-AD^2=DF^2+\left(AB+AF\right)^2-DF^2-AF^2=\)
\(=AB^2+AF^2+2AB.AF-AF^2=AB\left(AB+2AF\right)=AB.CD\)