Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1000x1003}{1001x1002}\),\(\frac{1001x1002}{1003x1001}\),\(\frac{1000x1002}{1003x1001}\)
0.999998006 ,0.999002991 ,0.998004986
vậy \(\frac{1000x1003}{1001x1002}\)là ps lớn nhất

\(\frac{2020}{2027}=1-\frac{7}{2027}\)
\(\frac{2027}{2034}=1-\frac{7}{2034}\)
Vì \(\frac{7}{2027}>\frac{7}{2034}\)
Nên \(1-\frac{7}{2027}< 1-\frac{7}{2034}\)
Vậy \(\frac{2020}{2027}< \frac{2027}{2034}\)
\(\text{Ta có :}\)
\(\frac{2020}{2027}=1-\frac{7}{2027}\)
\(\frac{2027}{2034}=1-\frac{7}{2034}\)
\(\text{VÌ }\frac{7}{2027}>\frac{7}{2034}\text{ nên }1-\frac{7}{2027}< 1-\frac{7}{2034}\)
\(\text{Vậy }\frac{2020}{2027}< \frac{2027}{2034}\)

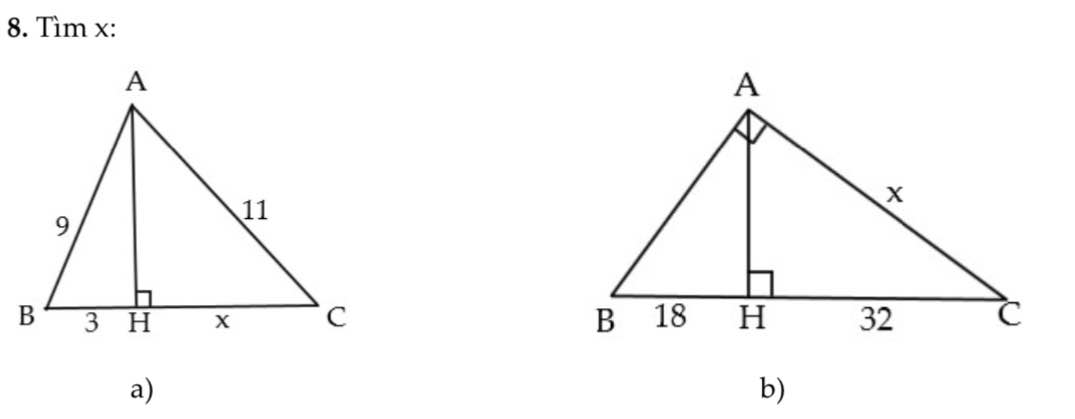
a, Theo định lí Pytago tam giác ABH vuông tại H
\(AH=\sqrt{AB^2-BH}=\sqrt{81-9}=6\sqrt{2}\)
Theo định lí Pytago tam giác AHC vuông tại H
\(HC=x=\sqrt{AC^2-AH^2}=7\)
b, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AC^2=HC.BC=1600\Rightarrow AC=x=40\)


1)Ta có: A= 2004/2005=1- 1/2005 B=2005/2006=1- 1/2006 1/2005>1/2006 =>1- 1/2005 < 1- 1/2006
Vậy A<B.
2)Tương tự như trên,1001/1002<1002/1003

CÓ:
Xét \(\Delta\)AEC có: \(\widehat{ACE}=180^o-\widehat{AEC}-\widehat{EAC}\)
Xét \(\Delta\)ADB có: \(\widehat{ABD}=180^o-\widehat{ADB}-\widehat{DAB}\)
Mà \(\widehat{AEC}=\widehat{ADB}\left(gt\right);\widehat{EAC}=\widehat{DAB}\left(=\widehat{BAC}\right)\)
=> \(\widehat{ACE}=\widehat{ABD}\)
=> \(2.\widehat{ACE}=2.\widehat{ABD}\)
=> \(\widehat{ABC}=\widehat{ACB}.\)

(1001 + 1002 + 1003 + ... + 2012).(360.87 - 720.16 - 360.55)
= (1001 + 1002 + 1003 + ... + 2012).(360.87 - 360.2.16 - 360.55)
= (1001 + 1002 + 1003 + ... + 2012).(360.87 - 360.32 - 360.55)
= (1001 + 1002 + 1003 + ... + 2012).[360.(87-32-55)]
= (1001 + 1002 + 1003 + ... + 2012).(360.0)
= (1001 + 1002 + 1003 + ... + 2012).0
= 0 ( vì 0 nhân bất kì số nào cũng bằng 0)
\(\frac{1001}{1000}\)và \(\frac{1002}{1003}\)
Giải
Vì
\(\frac{1001}{1000}\)\(>1\)
\(\frac{1002}{1003}\)\(< 1\)
Nên
\(\frac{1001}{1000}\)\(>\frac{1002}{1003}\)
Hok tốt
Ta thấy
\(\frac{1001}{1000}>1\)
\(\frac{1002}{1003}< 1\)
Nên :
\(\frac{1001}{1000}>\frac{1002}{1003}\)