NV
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
5
17 tháng 7 2021
\(\frac{2020}{2027}=1-\frac{7}{2027}\)
\(\frac{2027}{2034}=1-\frac{7}{2034}\)
Vì \(\frac{7}{2027}>\frac{7}{2034}\)
Nên \(1-\frac{7}{2027}< 1-\frac{7}{2034}\)
Vậy \(\frac{2020}{2027}< \frac{2027}{2034}\)
17 tháng 7 2021
\(\text{Ta có :}\)
\(\frac{2020}{2027}=1-\frac{7}{2027}\)
\(\frac{2027}{2034}=1-\frac{7}{2034}\)
\(\text{VÌ }\frac{7}{2027}>\frac{7}{2034}\text{ nên }1-\frac{7}{2027}< 1-\frac{7}{2034}\)
\(\text{Vậy }\frac{2020}{2027}< \frac{2027}{2034}\)
B
2
27 tháng 1 2022
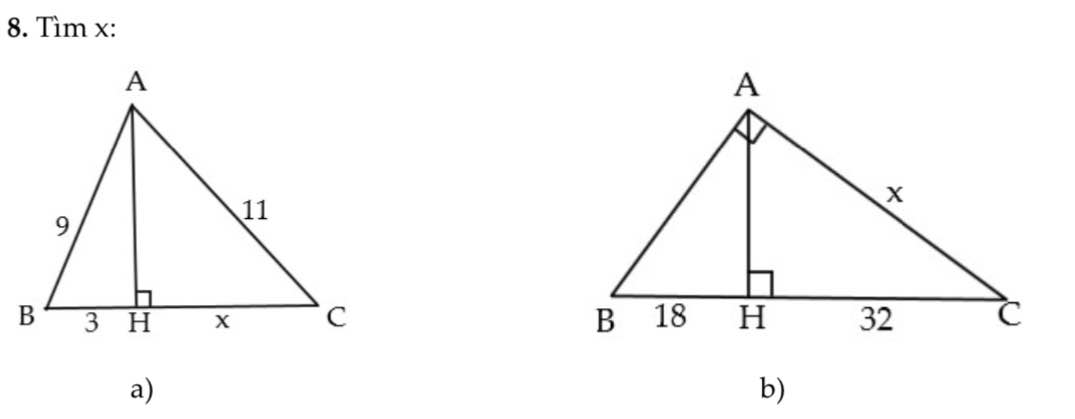
a, Theo định lí Pytago tam giác ABH vuông tại H
\(AH=\sqrt{AB^2-BH}=\sqrt{81-9}=6\sqrt{2}\)
Theo định lí Pytago tam giác AHC vuông tại H
\(HC=x=\sqrt{AC^2-AH^2}=7\)
b, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AC^2=HC.BC=1600\Rightarrow AC=x=40\)
VT
0
27 tháng 10 2019
CÓ:
Xét \(\Delta\)AEC có: \(\widehat{ACE}=180^o-\widehat{AEC}-\widehat{EAC}\)
Xét \(\Delta\)ADB có: \(\widehat{ABD}=180^o-\widehat{ADB}-\widehat{DAB}\)
Mà \(\widehat{AEC}=\widehat{ADB}\left(gt\right);\widehat{EAC}=\widehat{DAB}\left(=\widehat{BAC}\right)\)
=> \(\widehat{ACE}=\widehat{ABD}\)
=> \(2.\widehat{ACE}=2.\widehat{ABD}\)
=> \(\widehat{ABC}=\widehat{ACB}.\)
H
26 tháng 2 2020
Theo bài ra ta có :
\(A=\frac{2011}{1.2}+\frac{2011}{3.4}+\frac{2011}{4.5}+...+\frac{2011}{1999.2000}\)
\(\Rightarrow\frac{A}{2011}=\frac{1}{1.2}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{1999.2000}\)
\(\Rightarrow\frac{A}{2011}=\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{1999}-\frac{1}{2000}\)
\(\Rightarrow\frac{A}{2011}=\left(\frac{1}{1}+\frac{1}{3}+...+\frac{1}{1999}\right)+\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{2000}\right)\)
\(\Rightarrow\frac{A}{2011}=\left(\frac{1}{1}+\frac{1}{2}+...+\frac{1}{2000}\right)-\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{2000}\right)\) \(-\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{2000}\right)\)
\(\Rightarrow\frac{A}{2011}=\left(\frac{1}{1}+\frac{1}{2}+...+\frac{1}{2000}\right)-2\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{2000}\right)\)
\(\Rightarrow\frac{A}{2011}=\left(\frac{1}{1}+\frac{1}{2}+...+\frac{1}{2000}\right)-\left(\frac{1}{1}+\frac{1}{2}+...+\frac{1}{1000}\right)\)
\(\Rightarrow\frac{A}{2011}=\frac{1}{1001}+\frac{1}{1002}+...+\frac{1}{2000}\)
\(\Rightarrow A=2011\left(\frac{1}{1001}+\frac{1}{1002}+...+\frac{1}{2000}\right)\left(1\right)\)
Ta lại có :
\(B=\frac{2012}{1001}+\frac{2012}{1002}+...+\frac{2012}{2000}\)
\(\Rightarrow B=2012\left(\frac{1}{1001}+\frac{1}{1002}+...+\frac{1}{2000}\right)\)\(\left(2\right)\)
Từ (1) và (2) => A < B
Vậy A < B
DN
2
9 tháng 3 2023
\(\text{#TNam}\)
`5,A`
Gọi các cạnh của Tam giác `ABC` lần lượt là `x,y,z (x,y,z \ne 0)`
`3` góc của tam giác lần lượt tỉ lệ với `2:3:4`
Nghĩa là: `x/2=y/3=z/4`
Tổng số đo `3` góc trong `1` tam giác là `180^0`
`-> x+y+z=180`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2=y/3=z/4=`\(\dfrac{x+y+z}{2+3+4}=\dfrac{180}{9}=20\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{2}=20\\\dfrac{y}{3}=20\\\dfrac{z}{4}=20\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=20\cdot2=40\\y=20\cdot3=60\\z=20\cdot4=80\end{matrix}\right.\)
Vậy, độ dài các cạnh của Tam giác `ABC` lần lượt là `40^0, 60^0, 80^0`.
`6,B`
Gọi số người thợ của `3` nhóm lần lượt là `x,y,z (x,y,z \ne 0)`
Vì năng suất làm việc của các người thợ như nhau `->` số thợ và số ngày là `2` đại lượng tỉ lệ nghịch
`-> 40x=60y=50z` hay \(\dfrac{x}{\dfrac{1}{40}}=\dfrac{y}{\dfrac{1}{60}}=\dfrac{z}{\dfrac{1}{50}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{\dfrac{1}{40}}=\dfrac{y}{\dfrac{1}{60}}=\dfrac{z}{\dfrac{1}{50}}=\dfrac{x-z}{\dfrac{1}{40}-\dfrac{1}{50}}=\dfrac{3}{\dfrac{1}{200}}=600\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{\dfrac{1}{40}}=600\\\dfrac{y}{\dfrac{1}{60}}=600\\\dfrac{z}{\dfrac{1}{50}}=600\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=600\cdot\dfrac{1}{40}=15\\y=600\cdot\dfrac{1}{60}=10\\z=600\cdot\dfrac{1}{50}=12\end{matrix}\right.\)
Vậy, số thợ của nhóm `1,2,3` lần lượt là `15,10,12`.
TC
Cho số b = \(3^{1001}.7^{1002}.13^{1003}\) . Tìm chữ số hàng đơn vị của số b
Giúp Thảo nha. Thảo addf
3
4 tháng 9 2016
\(3^{1001}.7^{1002}.13^{1003}\)
\(=3^{1000}.3.7^{1000}.7^2.13^{1000}.13^3\)
\(=\left(3^4\right)^{250}.\left(7^4\right)^{250}.\left(13^4\right)^{250}.3.49.......7\)
\(=.......1.......1......1.3.49...7\)
\(=....9\)
Vậy chữ số tận cùng đơn vị của số b là 9
IM
4 tháng 9 2016
Ta có
\(b=3^{1001}.7^{1002}.13^{1003}\)
\(\Rightarrow b=\left(3^4\right)^{500}.3.\left(7^4\right)^{500}.7^2.\left(13^4\right)^{500}.13^3\)
\(\Rightarrow b=\left(\overline{.....1}\right).3.\left(\overline{.....1}\right).49.\left(\overline{......1}\right).2197\)
\(\Rightarrow b=\left(\overline{.....1}\right).\left(\overline{.....9}\right)\)
\(\Rightarrow b=\left(\overline{.....9}\right)\)
Vậy chữ số hàng đơn vị của b là 9
\(\frac{1001}{1000}\)và \(\frac{1002}{1003}\)
Giải
Vì
\(\frac{1001}{1000}\)\(>1\)
\(\frac{1002}{1003}\)\(< 1\)
Nên
\(\frac{1001}{1000}\)\(>\frac{1002}{1003}\)
Hok tốt
Ta thấy
\(\frac{1001}{1000}>1\)
\(\frac{1002}{1003}< 1\)
Nên :
\(\frac{1001}{1000}>\frac{1002}{1003}\)