a)Tìm giá trị nhỏ nhất của A=x
4+y4
b)Tìm giá trị lớn nhất của C=xy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. Áp dụng BĐT Cô-si:
$x^4+9\geq 6x^2$
$y^4+9\geq 6y^2$
$\Rightarrow x^4+y^4+18\geq 6(x^2+y^2)$
$A+18\geq 36$
$A\geq 18$
Vậy GTNN của $A$ là $18$ khi $x^2=y^2=3$
b.
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 2(x^2+y^2)\geq (x+y)^2$
$\Leftrightarrow 12\geq (x+y)^2$
$\Rightarrow B=x+y\leq \sqrt{12}$. Vậy $B$ max bằng $\sqrt{12}$ khi $x=y=\sqrt{3}$
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 6\geq 2C$
$\Leftrightarrow C\leq 3$. Vậy $C_{\max}=3$. Giá trị này đạt tại $x=y=-\sqrt{3}$

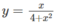 trên khoảng (−
∞
;+
∞
);
trên khoảng (−
∞
;+
∞
);
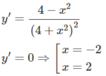
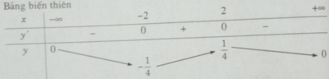
Từ đó ta có min f(x) = −1/4; max f(x) = 1/4

Tập xác định D = [0; 1]
Ta có:
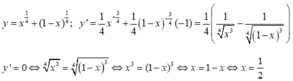
y(0) = y(1) = 1; y 1 2 = 8 4 . Từ đó max m a x y = 8 4 , m i n y = 1 , min y = y(0) = 1
Chọn C

\(A=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\\ A_{min}=4\Leftrightarrow x=1\\ B=2\left(x^2-3x\right)=2\left(x^2-2\cdot\dfrac{3}{2}x+\dfrac{9}{4}\right)-\dfrac{9}{2}\\ B=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\\ B_{min}=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{3}{2}\\ C=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\\ C_{max}=7\Leftrightarrow x=2\)
a,\(A=x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
Dấu "=" \(\Leftrightarrow x=-1\)
b,\(B=2\left(x^2-3x\right)=2\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{2}=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
Dấu "=" \(\Leftrightarrow x=\dfrac{3}{2}\)
c,\(=C=-\left(x^2-4x-3\right)=-\left[\left(x^2-4x+4\right)-7\right]=-\left(x-2\right)^2+7\le7\)
Dấu "=" \(\Leftrightarrow x=2\)

a) \(a+b=2\)
=> \(b=2-a\)
\(A=a^2+\left(2-a\right)^2=2a^2-4a+4=\left(\sqrt{2}a-\sqrt{2}\right)^2+2\ge2\)
Vậy \(A_{min}=2\)
b) \(x+2y=8\)
=> \(x=8-2y\)
\(B=y\left(8-2y\right)=8y-2y^2=8-\left(\sqrt{2}y-2\sqrt{2}\right)^2\le8\)
Vậy \(B_{max}=8\)
a) \(\left(a-b\right)^2\ge0\Leftrightarrow a^2+b^2\ge2ab\Leftrightarrow2\left(a^2+b^2\right)\ge a^2+b^2+2ab\)
\(\Leftrightarrow a^2+b^2\ge\frac{\left(a+b\right)^2}{2}=\frac{2^2}{2}=2\)
Dấu \(=\)khi \(a=b=1\).
b) \(\left(x-2y\right)^2\ge0\Leftrightarrow x^2+4y^2\ge4xy\Leftrightarrow x^2+4xy+4y^2\ge8xy\)
\(\Leftrightarrow xy\le\frac{\left(x+2y\right)^2}{8}=\frac{8^2}{8}=8\)
Dấu \(=\)khi \(\hept{\begin{cases}x=4\\y=2\end{cases}}\).
Đề sai rồi bạn