Bài 1: Cho tam giác abc cân ở a , phân giác BD , BC=10cm , AB=15
a) tính AD , DC
b) đg phân giác ngoài b của tam giác abc cắt AC tại D' . Tính D'
cần phần b:((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 3 2020
a)
Vì BD là đường phân giác của \(\widehat{ABC}\) nên:
\(\frac{AD}{DC}=\frac{AB}{BC}\)(tính chất đường phân giác )
\(\Rightarrow\frac{AD}{AD+DC}=\frac{AB}{AB+BC}\)hay \(\frac{AD}{AC}=\frac{AB}{AB+BC}\)
Mà \(\Delta\)ABC cân tại A nên AC=AB=15cm
\(\Rightarrow\frac{AD}{15}=\frac{15}{15+10}\Rightarrow AD=\frac{15\cdot15}{25}=9\left(cm\right)\)
Vậy DC = AC – AD = 15 – 9 = 6 (cm)
PG
12 tháng 2 2020
EZ thôi,vài đường cơ bản;gộp lại cho nó máu ! À mà tính BD chứ nhỉ ??
Kẻ CE là phân giác góc C cắt BD tại E
Đặt EC=x thì BE=x;đặt ED=y
Áp dụng tính chất đường phân giác ta có:
\(\frac{DA}{DC}=\frac{AB}{BC}=\frac{15}{10}=\frac{3}{2}\left(cm\right)\) khi đó \(DA=3a;DC=2a\)
Ta có:\(15=AC=DA+DC=3a+2a=5a\Rightarrow a=3\)
\(\Rightarrow DA=9;DC=6\)
Dễ thấy \(\Delta EDC~\Delta CDB\left(g.g\right)\Rightarrow\frac{ED}{CD}=\frac{DC}{DB}=\frac{EC}{CB}\)
hay \(\frac{y}{6}=\frac{6}{BD}=\frac{x}{10}=\frac{x+y}{10+6}=\frac{x+y}{16}=\frac{BD}{16}\)
\(\Rightarrow BD^2=96\Rightarrow BD=\sqrt{96}\) số khá xấu,ko bt có nhầm lẫn đâu chăng ??
HH
9 tháng 7 2020
1)
Kẻ AH là đường cao của ABC
Ta có :\(S_{ABCD}=\frac{1}{2}.AH.BD ; S_{ADC}=\frac{1}{2}.AH.CD\)
\(\Rightarrow\frac{S_{ABC}}{S_{ADC}}=\frac{\frac{1}{2}.AH.BD}{\frac{1}{2}.AH.CD}=\frac{BD}{CD}\left(1\right)\)
\(\Delta ABC\)có AD là tia phân giác
\(\Rightarrow\frac{BD}{CD}=\frac{AB}{AC}\left(2\right)\)
Từ (1)(2)
\(\Rightarrow\frac{S_{ABCD}}{S_{ACD}}=\frac{AB}{AC}=\frac{m}{n}\)
Vậy tỉ số của tam giác ABD và ACD là \(\frac{m}{n}\)
Lời giải:
a. Vì $ABC$ cân tại $A$ nên $AC=AB=15$
Theo tính chất tia phân giác: $\frac{AD}{DC}=\frac{AB}{BC}=\frac{15}{10}=\frac{3}{2}$
$\Leftrightarrow \frac{AD}{AC}=\frac{3}{5}$
$\Leftrightarrow \frac{AD}{15}=\frac{3}{5}$
$\Rightarrow AD=9$
$DC=AC-AD=15-9=6$
b. Tính D' gì hả bạn? D'C hay D'B, D'A?
Theo tính chất phân giác ngoài:
$\frac{D'C}{D'A}=\frac{BC}{BA}=\frac{10}{15}=\frac{2}{3}$
$\Leftrightarrow \frac{D'C}{D'C+CA}=\frac{D'C}{D'C+15}=\frac{2}{3}$
$\Rightarrow 3D'C=2(D'C+15)$
$\Rightarrow D'C=30$ (cm)
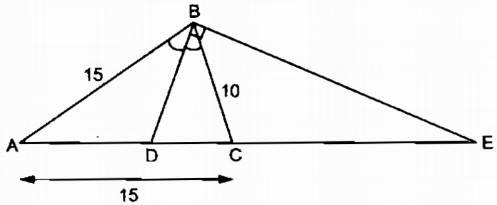
Hình vẽ:
