Cho tam giác 𝐴𝐵𝐶 có ba góc nhọn, đường cao 𝐵𝐸. Từ E kẻ 𝐸𝐻, 𝐸𝐾 vuông góc với 𝐵𝐴, 𝐵𝐶. a) Chứng minh 𝐵𝐻. 𝐵𝐴 = 𝐵𝐾. 𝐵𝐶 b) Chứng minh ∆𝐵𝐻𝐾~∆𝐵𝐶𝐴. c) Kẻ 𝐶𝐹 vuông góc với 𝐴𝐵, gọi 𝐼 là trung điểm của 𝐸𝐹. Chứng minh ba điểm 𝐻,𝐼,𝐾 thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xet ΔABC và ΔEBA có
góc BAC=góc BEA
góc B chung
=>ΔABC đồng dạng với ΔEBA
b: ΔABC vuông tại A có AE vuông góc BC
nên AB^2=BE*BC
c: BF là phân giác
=>AF/AB=CF/BC
=>AF/3=FC/5=4/8=1/2
=>AF=1,5cm

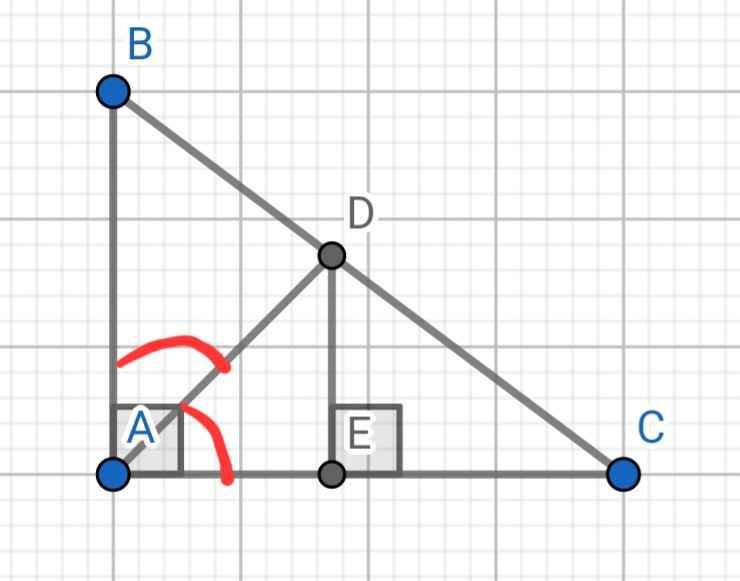
a) Do AD là đường phân giác của ∠BAC
⇒ BD/CD = AB/AC = 9/12 = 3/4
b) Xét hai tam giác vuông: ∆ABC và ∆EDC có:
∠C chung
⇒ ∆ABC ∽ ∆EDC (g-g)
a: BD/CD=AB/AC=3/4
b: Xét ΔABC vuông tại A và ΔEDC vuông tại E có
góc C chung
=>ΔABC đồng dạng với ΔEDC

a: Xét tứ giác BHCD có
CH//BD
BH//CD
Do đó: BHCD là hình bình hành

a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔCAB vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(CH\cdot CB=AC^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔCDB vuông tại C có CA là đường cao ứng với cạnh huyền DB, ta được:
\(AD\cdot AB=CA^2\left(2\right)\)
Từ (1) và (2) suy ra \(CH\cdot CB=AD\cdot AB\)
nho thay co giup em voi em dungf tu giac noi tiep khong dung

a: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
Xét ΔADE có AD=AE
nên ΔADE cân tại A
b: Xét ΔABC có
D là trung điểm của AB
DF//AC
Do đó: F là trung điểm của BC
Xét ΔABC có
D là trung điểm của AB
F là trung điểm của BC
Do đó: DF là đường trung bình
=>DF=AE
mà AE=AD
nên DF=AD
=>ΔADF cân tại D
c: Xét tứ giác ADFE có
DF//AE
DF=AE
Do đó: ADFE là hình bình hành
mà AD=AE
nên ADFE là hình thoi
=>AF⊥DE

Cho hình thoi 𝐴𝐵𝐶𝐷 (𝐴መ > 90). Gọi 𝐸 là hình chiếu vuông góc của 𝐴 trên 𝐵𝐶, 𝐹 là hình
chiếu vuông góc của 𝐶 trên 𝐴𝐷.
a) Tứ giác 𝐴𝐸𝐶𝐹 là hình gì? Vì sao?
b) 𝐵𝐷 cắt 𝐴𝐸 tại 𝐻, cắt 𝐶𝐹 tại 𝐾. Chứng minh rằng 𝐴𝐾 = 𝐶𝐻.
c) Gọi 𝐼 là giao điểm của 𝐴𝐾 và 𝐶𝐷, 𝐽 là giao điểm của 𝐶𝐻 và 𝐴𝐵. Chứng minh rằng 𝐸𝐼 ⊥ 𝐸𝐽

Bài 1:
a: Ta có: ΔBKC vuông tại K
mà KM là đường trung tuyến
nên KM=BC/2(1)
Ta có: ΔBHC vuông tại H
mà HM là đường trung tuyến
nên HM=BC/2(2)
Từ (1)và (2) suy ra MH=MK
hay ΔMHK cân tại M
b: Kẻ MN vuông góc với HK
=>N là trung điểm của HK
Xét hình thang CBDE có
M là trung điểm của BC
MN//DB//EC
DO đó: N là trung điểm của DE
=>DK=HE
a) tam giác AEB vuông tại E có EH là đường cao \(\Rightarrow BH.BA=BE^2\)
tam giác CEB vuông tại E có EK là đường cao \(\Rightarrow BK.BC=BE^2\)
\(\Rightarrow BH.BA=BK.BC\)
b) \(BH.BA=BK.BC\Rightarrow\dfrac{BH}{BC}=\dfrac{BK}{BA}\)
Xét \(\Delta BHK\) và \(\Delta BCA:\) Ta có: \(\left\{{}\begin{matrix}\angle ABCchung\\\dfrac{BH}{BC}=\dfrac{BK}{BA}\end{matrix}\right.\)
\(\Rightarrow\Delta BHK\sim\Delta BCA\left(c-g-c\right)\)
b) \(\Delta BHK\sim\Delta BCA\Rightarrow\angle BHK=\angle BCA\)
Kẻ \(ED\bot CF\)
Vì \(\angle EHF=\angle EDF=\angle HFD=90\Rightarrow EHFD\) là hình chữ nhật
\(\Rightarrow HD\) và EF cắt nhau tại trung điểm I của mỗi đường
Vì \(\Delta EHF\) vuông tại H có I là trung điểm EF
\(\Rightarrow\angle FHI=\angle HFI=\angle AFE\left(1\right)\)
Xét \(\Delta AFC\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle AFC=\angle AEB=90\end{matrix}\right.\)
\(\Rightarrow\Delta AFC\sim\Delta AEB\left(g-g\right)\Rightarrow\dfrac{AF}{AE}=\dfrac{AC}{AB}\Rightarrow\dfrac{AF}{AC}=\dfrac{AE}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ABC:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\dfrac{AF}{AC}=\dfrac{AE}{AB}\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c-g-c\right)\Rightarrow\angle AFE=\angle ACB\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\angle FHI=\angle ACB=\angle BHK\Rightarrow\angle BHD=BHK\)
\(\Rightarrow H,D,K\) thẳng hàng \(\Rightarrow H,I,K\) thẳng hàng
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔBEA vuông tại E có EH là đường cao ứng với cạnh huyền AB, ta được:
\(BH\cdot BA=BE^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBEC vuông tại E có EK là đường cao ứng với cạnh huyền AC, ta được:
\(BK\cdot BC=BE^2\)(2)
Từ (1) và (2) suy ra \(BH\cdot BA=BK\cdot BC\)
b) Xét ΔBHK và ΔBCA có
\(\dfrac{BH}{BC}=\dfrac{BK}{BA}\)(cmt)
\(\widehat{HBK}\) chung
Do đó: ΔBHK\(\sim\)ΔBCA(c-g-c)