Cho tam giác ABC cân tại A, BD là đường cao, E là trung điểm của BC, H là giao điểm của
AE và BD.
a) Chứng minh 4 điểm A, D, E, B cùng thuộc đường tròn tâm O.
b) Xác định tâm I của đường tròn đi qua 3 điểm H, D, C.
c) Chỉ ra 2 điểm chung của đường tròn tâm (O) và đường tròn (I).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 7 2021
a) Ta có: ΔABC cân tại A(gt)
mà AE là đường trung tuyến ứng với cạnh BC(gt)
nên AE là đường cao ứng với cạnh BC(Định lí tam giác cân)
Xét tứ giác ABED có
\(\widehat{AEB}=\widehat{ADB}\left(=90^0\right)\)
nên ABED là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay A,B,E,D cùng thuộc (O)
b) Xét tứ giác HDCE có
\(\widehat{HEC}+\widehat{HDC}=180^0\)
nên HDCE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Tâm I của đường tròn ngoại tiếp tứ giác HDCE là trung điểm của HC
17 tháng 3 2023
a: góc ADH+góc AEH=180 độ
=>ADHE nội tiếp
O là trung điểm của AH
b:
XetΔACB có
BD,CE là đường cao
BD căt CE tại H
=>H là trực tâm
=>AH vuông góc BC
=>K là trung điểm của CB
góc ODK=góc ODH+góc KDH
=góc BHK+góc KBH=90 độ
=>KD là tiếp tuyến của (O)
16 tháng 9 2019
a. Gọi O là trung điểm AB
Tam giác ADB vuông tại D
=> Tam giác ADB nội tiếp đường tròn tâm O, đường kính AB (1)
Tam giác ABC cân tại A có AE là trung tuyến
=> AE cũng là đường cao của tam giác
=>AE vuông góc BC
Tam giác AEB vuông tại E
=>Tam giác AEB nội tiếp đường tròn tâm O, đường kính AB (2)
(1)(2) => A,D,B,E cùng thuộc đường tròn tâm O, đường kính AB
b. Tam giác HCD vuông tại D
=>Tam giác HCD nội tiếp đường tròn đường kính HC
=>Tâm O' của đường tròn đi qua 3 điểm H,C,D là trung điểm của cạnh HC.
26 tháng 9 2017
a)Nối F với D : E với D ta có:
Xét tam giác FBC ta có
D là trung điểm BC(1)
Góc BFC=90 (2)
Từ (1)(2)=>FD là trung tuyến của tam giác FBC
=>BD=CD=DF(*)
Chứng minh tương tự tam giác EBC
=>DE=DC=DB(**)
Từ (*)(**)=>BD=CD=DF=DE=(1/2BC)
=>B;F;E;C thuộc đừng tròn
=>D là tâm của đường tròn
B) Do B;H;E nằm trên cùng 1 đừng thẳng => H ko thuộc đừng tròn
=>B;H;E;c ko thuộc đừng tròn
28 tháng 11 2023
a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó;ΔBEC vuông tại E
=>CE\(\perp\)BE tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó;ΔBDC vuông tại D
=>BD\(\perp\)DC tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
b: Xét tứ giác AEHD có \(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)
=>AEHD là tứ giác nội tiếp đường tròn đường kính AH
=>A,E,H,D cùng nằm trên đường tròn đường kính AH
c: I là tâm của đường tròn đi qua 4 điểm A,E,H,D
=>I là trung điểm của AH
Gọi giao điểm của AH với BC là M
AH\(\perp\)BC
nên AH\(\perp\)BC tại M
\(\widehat{BHM}=\widehat{IHD}\)
mà \(\widehat{IHD}=\widehat{IDH}\)(ID=IH)
nên \(\widehat{BHM}=\widehat{IDH}\)
mà \(\widehat{BHM}=\widehat{BCD}\left(=90^0-\widehat{HBM}\right)\)
nên \(\widehat{IDH}=\widehat{BCD}\)
OB=OD
=>ΔODB cân tại O
=>\(\widehat{OBD}=\widehat{ODB}\)
=>\(\widehat{ODH}=\widehat{DBC}\)
\(\widehat{IDO}=\widehat{IDH}+\widehat{ODH}\)
\(=\widehat{DBC}+\widehat{DCB}\)
\(=90^0\)
=>ID\(\perp\)DO
CM
24 tháng 8 2018
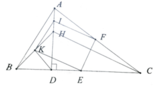
a, Chứng minh IFEK là hình bình hành có tâm O. Chứng minh IK ⊥ KE => IFEKlà hình chữ nhật => I,F,E,K cùng thuộc (O;OI)
b, Ta có: I D E ^ = 90 0 => Tam giác IDE vuông tại D
Chứng minh rằng KD ⊥ DF => ∆ KDF vuông
23 tháng 7 2023
a:
góc BDC=góc BEC=1/2*sđ cung BC=90 độ
=>CD vuông góc AB và BE vuông góc AC
Xét ΔABC có
CD,BE là đường cao
CD cắt BE tại H
=>H là trực tâm
=>AH vuông góc BC
b: góc AEH+góc ADH=180 độ
=>AEHD nội tiếp đường tròn đường kính AH
=>I là trung điểm của AH
c: góc BDC=góc BEC=90 độ
=>BDEC nội tiếp đường tròn đường kính BC
=>O là trung điểm của BC
d: ID=IE
OD=OE
=>OI là trung trực của DE
=>OI vuông góc DE
19 tháng 8 2021
a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp
Tâm là trung điểm của BC
Bán kính là \(\dfrac{BC}{2}=\dfrac{a}{2}\)
a) Vì tam giác ABC cân tại A có E là trung điểm BC
\(\Rightarrow AE\bot BC\Rightarrow\angle AEB=90\)
\(\Rightarrow\angle AEB=\angle ADB=90\Rightarrow ADEB\) nội tiếp
b) Vì \(\angle HDC=90\Rightarrow\left(HDC\right)\) là đường tròn đường kính HC
\(\Rightarrow\) tâm I của (HDC) là trung điểm HC
c) Ta có: \(\angle HEC+\angle HDC=90+90=180\Rightarrow HDCE\) nội tiếp
\(\Rightarrow\left(I\right)\) đi qua điểm E và D
Vì ADEB nội tiếp \(\Rightarrow\left(O\right)\) đi qua điểm E và D
\(\Rightarrow\) 2 điểm chung là D và E