Cho x,y,z > 0 và xyz=1 . Tìm MinP = \(\Sigma\dfrac{1}{x^4\left(y+1\right)\left(z+1\right)}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Áp dụng BĐT AM-GM:
$\frac{x^3}{y(x+z)}+\frac{y}{2}+\frac{x+z}{4}\geq \frac{3}{2}x$
Tương tự với các phân thức còn lại, cộng theo vế và rút gọn ta được:
$\Rightarrow P=\sum \frac{x^3}{y(x+z)}\geq \frac{x+y+z}{2}$
Tiếp tục áp dụng AM-GM:
$x+y\geq 2\sqrt{xy}$
$y+z\geq 2\sqrt{yz}$
$x+z\geq 2\sqrt{xz}$
$\Rightarrow x+y+z\geq \sqrt{xy}+\sqrt{yz}+\sqrt{xz}=1$
$\Rightarrow P\geq \frac{1}{2}$
Vậy $P_{\min}=\frac{1}{2}$ khi $x=y=z=\frac{1}{3}$
\(\dfrac{x^3}{y\left(x+z\right)}+\dfrac{y}{2}+\dfrac{x+z}{4}\ge\dfrac{3x}{2}\)
Tương tự và cộng lại:
\(P+x+y+z\ge\dfrac{3}{2}\left(x+y+z\right)\)
\(\Rightarrow P\ge\dfrac{1}{2}\left(x+y+z\right)\ge\dfrac{1}{2}\left(\sqrt{xy}+\sqrt{yz}+\sqrt{zx}\right)=\dfrac{1}{2}\)

Câu hỏi của Đỗ Tuấn Linh - Toán lớp 9 - Học toán với OnlineMath

\(P\le\sqrt{3\left(\sum\dfrac{1}{\left(x+y\right)^2+\left(x+1\right)^2+4}\right)}\le\sqrt{3\left(\sum\dfrac{1}{4xy+4x+4}\right)}\)
\(P\le\sqrt{\dfrac{3}{4}\sum\left(\dfrac{1}{xy+x+1}\right)}=\dfrac{\sqrt{3}}{2}\)
\(P_{max}=\dfrac{\sqrt{3}}{2}\) khi \(x=y=z=1\)

dễ mà bạn :))) gáy tí , sai thì thôi
\(P=\frac{x^3}{\left(1+x\right)\left(1+y\right)}+\frac{y^3}{\left(1+y\right)\left(1+z\right)}+\frac{z^3}{\left(1+z\right)\left(1+x\right)}\)
\(=\frac{x^3\left(1+z\right)}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}+\frac{y^3\left(1+x\right)}{\left(1+y\right)\left(1+x\right)\left(1+z\right)}+\frac{z^3\left(1+y\right)}{\left(1+x\right)\left(1+z\right)\left(1+y\right)}\)
\(=\frac{x^3\left(1+z\right)+y^3\left(1+x\right)+z^3\left(1+y\right)}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\ge\frac{3\sqrt[3]{x^3y^3z^3\left(1+x\right)\left(1+y\right)\left(1+z\right)}}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\)
đến đây áp dụng BĐT phụ ( 1+a ) ( 1+b ) ( 1+c ) >= 8abc
EZ :)))

\(P=\dfrac{1}{3x\left(y+z\right)+x+y+z}+\dfrac{1}{3y\left(z+x\right)+x+y+z}+\dfrac{1}{3z\left(x+y\right)+x+y+z}\)
\(P\le\dfrac{1}{3x\left(y+z\right)+3\sqrt[3]{xyz}}+\dfrac{1}{3y\left(z+x\right)+3\sqrt[3]{xyz}}+\dfrac{1}{3z\left(x+y\right)+3\sqrt[3]{xyz}}\)
\(P\le\dfrac{1}{3x\left(y+z\right)+3}+\dfrac{1}{3y\left(z+x\right)+3}+\dfrac{1}{3z\left(x+y\right)+3}\)
Đặt \(\left(x;y;z\right)=\left(a^3;b^3;c^3\right)\Rightarrow abc=1\)
\(\Rightarrow P\le\dfrac{1}{3}\left(\dfrac{1}{a^3\left(b^3+c^3\right)+1}+\dfrac{1}{b^3\left(c^3+a^3\right)+1}+\dfrac{1}{c^3\left(a^3+b^3\right)+1}\right)\)
\(\Rightarrow P\le\dfrac{1}{3}\left(\dfrac{1}{a^3bc\left(b+c\right)+1}+\dfrac{1}{b^3ac\left(a+c\right)+1}+\dfrac{1}{c^3ab\left(a+b\right)+1}\right)\)
\(\Rightarrow P\le\dfrac{1}{3}\left(\dfrac{bc}{a\left(b+c\right)+bc}+\dfrac{ac}{b\left(a+c\right)+ac}+\dfrac{ab}{c\left(a+b\right)+ab}\right)=\dfrac{1}{3}\)
\(P_{max}=\dfrac{1}{3}\) khi \(a=b=c=1\) hay \(x=y=z=1\)

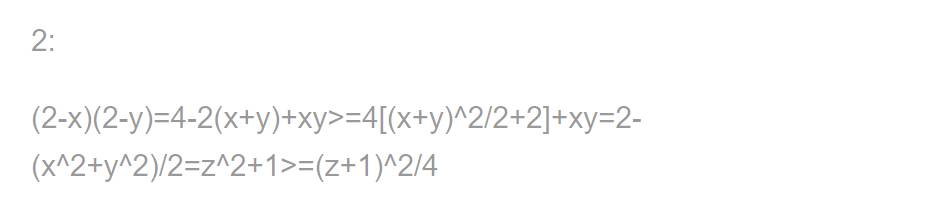
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM
Đặt \(\left(x;y;z\right)=\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)\Rightarrow abc=1\)
\(P=\sum\dfrac{a^4}{\left(\dfrac{1}{b}+1\right)\left(\dfrac{1}{c}+1\right)}=\sum\dfrac{a^4bc}{\left(b+1\right)\left(c+1\right)}=\sum\dfrac{a^3}{\left(b+1\right)\left(c+1\right)}\)
Ta có:
\(\dfrac{a^3}{\left(b+1\right)\left(c+1\right)}+\dfrac{b+1}{8}+\dfrac{c+1}{8}\ge\dfrac{3a}{4}\)
Tương tự và cộng lại:
\(P+\dfrac{a+b+c}{4}+\dfrac{3}{4}\ge\dfrac{3\left(a+b+c\right)}{4}\Rightarrow P\ge\dfrac{a+b+c}{2}-\dfrac{3}{4}\ge\dfrac{3}{2}-\dfrac{3}{4}=\dfrac{3}{4}\)