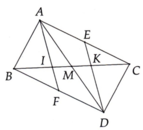
cho tam giác abc cân tại a, góc a < 90 độ. trên tia đối của tia ab lấy điểm d sao cho ad=ab. kẻ đường cao af của tam giác acd, ac cắt bf tại g.
a. chứng minh f là trung điểm của dc và g là trọng tâm của tam giác bdc. chứng minh bd=6ag
b. kẻ ch vuông góc với bd(h thuộc bd), dk vuông góc với ca (k thuộc tia ca). chứng minh các đường thẳng af, ch, dk đồng quy
c. ke cắt ad tại i. biết góc bac=45 độ . so sánh độ dài các đoạn thẳng ch, hi, và id
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔAFC vuông tại F và ΔAFD vuông tại F có
AC=AD(=AB)
AF chung
Do đó: ΔAFC=ΔAFD(Cạnh huyền-cạnh góc vuông)
Suy ra: FC=FD(hai cạnh tương ứng)
mà C,F,D thẳng hàng(gt)
nên F là trung điểm của CD
Xét ΔBCD có
CA là đường trung tuyến ứng với cạnh BD(gt)
BF là đường trung tuyến ứng với cạnh DC(cmt)
CA cắt BF tại G(gt)
Do đó: G là trọng tâm của ΔBDC(Tính chất ba đường trung tuyến của tam giác)
\(\Leftrightarrow AG=\dfrac{1}{3}AC\)(Tính chất trọng tâm của tam giác)
mà \(AC=\dfrac{1}{2}BD\left(=AB\right)\)
nên \(AG=\dfrac{1}{3}\cdot\dfrac{1}{2}BD=\dfrac{1}{6}BD\)
hay BD=6AG(đpcm)

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
b) Xét ΔABH vuông tại H và ΔDCH vuông tại H có
BH=CH(ΔABH=ΔACH)
AH=DH(cmt)
Do đó: ΔABH=ΔDCH(hai cạnh góc vuông)
Suy ra: AB=DC(hai cạnh tương ứng)
mà AB=AC(ΔABC cân tại A)
nên DC=AC(Đpcm)

gggggjjjk..hhhyh iuugln............................lklhuluiiiihhhhhhh ok-