Cho góc xOy và điểm A nằm trong góc đó. Vẽ điểm B đối xứng với O qua A. Qua B vẽ
đường thẳng song song với Ox, cắt Oy ở C. Gọi D là giao điểm của CA và Ox. Chứng minh
rằng các điểm C và D đối xứng với nhau qua điểm A.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

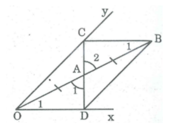
Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.

a: Ta có: B đối xứng với A qua Ox
nên OA=OB(1)
Ta có: C đối xứng với A qua Oy
nên OA=OC(2)
Từ (1) và (2) suy ra OB=OC

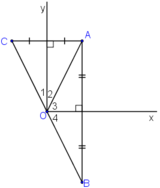
+ B đối xứng với A qua Ox
⇒ Ox là đường trung trực của AB
⇒ OA = OB (1)
+ C đối xứng với A qua Oy
⇒ Oy là đường trung trực của AC
⇒ OA = OC (2)
Từ (1) và (2) suy ra OB = OC (*).
+ Xét ΔOAC cân tại O (do OA = OC) có Oy là đường trung trực
⇒ Oy đồng thời là đường phân giác
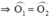
Xét ΔOAB cân tại O có Ox là đường trung trực
⇒ Ox đồng thời là đường phân giác
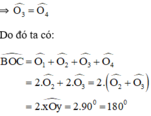
⇒ B, O, C thẳng hàng (**)
Từ (*) và (**) suy ra O là trung điểm BC
⇒ B đối xứng với C qua O.

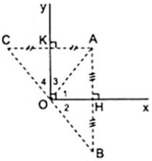
Vẽ AH ⊥ Ox, AK ⊥ Oy
Vẽ hai điểm B, C sao cho H, K lần lượt là trung điểm của AB, AC thì B là điểm đối xứng với A qua Ox, C là điểm đối xứng với A qua Oy.
Vì O ∈ Ox, O ∈ Oy nên O đối xứng với O qua Ox, Oy.
Áp dụng tính chất của phép đối xứng ta được
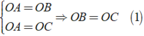
Và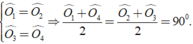
⇒ B O C ^ = 180 0 . ( 2 )
Từ ( 1 ), ( 2 ) suy ra O là trung điểm của BC hay B đối xứng với C qua O.
